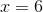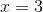To more easily solve for x, we need to try to express the right hand side of the equation in terms of a number of base 4. 256 is simply .

Rewriting the equation with this discovery yields

Since both bases are the same, we can set the exponents equal to each other and solve for x.

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this with a fraction, factor the denominator then use the laws of exponents to eliminate the fraction. For this problem that looks as follows:

Manipulate the fraction:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number in the denominator then manipulate the fraction until it looks like the left side of the equation. For this problem that looks as follows:

Factor the larger number and manipulate the fraction:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, divide both sides by the coefficient in order to get the exponent by itself. Then factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Divide both sides by 3:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same:

In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, divide both sides by the coefficient in order to get the exponent by itself. Then factor the larger number until it looks like the smaller one. For this problem that looks as follows:

Divide both sides by 2:

Factor the larger number:

Now substitute in the factored number:

Since the bases are now the same: