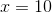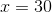We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Absolute Value Equations

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #81 : Solving Equations And Inequallities

Solve the following

$\left | 3x-5\right |=20$

Possible Answers:

There are no solutions

x=-5

$x=\frac{25}{3}$

x=-5

$x=\frac{25}{3}$

Correct answer:

x=-5

$x=\frac{25}{3}$

Explanation:

We have to set up two equations, which are.

3x-5=20

3x-5=-20

Now lets solve for x in each equation.

3x-5=20

$3x=25\rightarrow x=\frac{25}{3}$

3x-5=-20

$3x=-15\rightarrow x=-5$

So the solutions are x=-5 and $x=\frac{25}{3}$

Report an Error

Example Question #82 : Solving Equations And Inequallities

Solve:

|x-10|=20

Possible Answers:

x=-30

x=10

x=-30

x=-10

x=30

x=10

x=30

x=-10

Correct answer:

x=30

x=-10

Explanation:

We need to set up two equations since we are dealing with absolute value

$\\x-10=20\\x-10=-20$

We solve for , in each equation to get the solutions.

x=20+10=30

x=-20+10=-10

Report an Error

Example Question #83 : Solving Equations And Inequallities

Solve:

|x-45|=2

Possible Answers:

x=43

x=47

x=-43

x=-47

x=-43

x=47

x=43

x=-47

Correct answer:

x=43

x=47

Explanation:

We need to set up two equations since we are dealing with absolute value

$\\x-45=2\\x-45=-2$

We solve for , in each equation to get the solutions.

x=2+45=47

x=-2+45=43

Report an Error

Example Question #84 : Solving Equations And Inequallities

Solve the following:

$\left | x-2 \right |>1$

Possible Answers:

$(-\infty,-1)\cup (3, \infty)$

(1,3)

$(-\infty,1)\cup (3, \infty)$

$(-\infty,-3)\cup (-1, \infty)$

Correct answer:

$(-\infty,1)\cup (3, \infty)$

Explanation:

To solve, you must split the absolute value into the two following equations.

x-2>1 and x-2<-1

Now, solve for x and right it in interval form.

$x-2>1\Rightarrow x>3$

$x-2<-1\Rightarrow x<1$

$(-\infty,1)\cup (3,\infty)$

Report an Error

Example Question #81 : Solving Equations And Inequallities

Solve for x:

$\left | x-7 \right | = 3$

Possible Answers:

$x=-10\;; \; x=4$

$x = 10, \; \; x=4$

$x=4, \;\; x=-4$

$x=10\; ; \; x=-10$

Correct answer:

$x = 10, \; \; x=4$

Explanation:

To solve $\left | x-7\right | = 3$ we need to find a way to reverse the operation of taking the absolute value. What we need to do is think about what the absolute value operation does to an expression. Since it makes everything positive, $\left | x-7\right | = \left | (-1) (x-7)\right |$ . So actually solving the original equation comes down to solving the following two equations:

x-7=3

-(x-7)=3

So we get the two solutions as:

x=7+3=10

x=7-3=4

Report an Error

Example Question #4 : Absolute Value Equations

Solve the following equation for .

$\left |x^2-8 \right |=1$

Possible Answers:

$x=3,\sqrt{7}$

$x=\pm7,\pm\sqrt{3}$

$x=\pm3,\pm\sqrt{7}$

$x=\sqrt3,{-7}$

$x=\pm4,\pm2$

Correct answer:

$x=\pm3,\pm\sqrt{7}$

Explanation:

We first need to get rid of the absolute value symbol to solve the equation. TO break this absolute value, we assign two values to the right hand side, as shown below.

x^2-8=1

x^2-8=-1

We now proceed to solve each equation independently.

Starting with the first equation, we get

x^2=9

$x=\pm3$

Now for the second equation,

x^2=7

$x=\pm\sqrt{7}$

Report an Error

Example Question #85 : Solving Equations And Inequallities

Simplify the radical:

$\frac{2\sqrt{20}}{\sqrt{4}}$

Possible Answers:

None of the other answers.

$2\sqrt{5}$

$\sqrt{5}$

$-5\sqrt{2}$

Correct answer:

$2\sqrt{5}$

Explanation:

To simplify the radical, break the radical in the numerator down into its factors. When doing so, the radical in the bottom will call with one from the numerator.

$\frac{2\sqrt{20}}{\sqrt{4}}=\frac{2\sqrt{4}\sqrt{5}}{\sqrt{4}}=2{\sqrt{5}}$

Report an Error

Example Question #6 : Absolute Value Equations

Solve the following equation:

$-3-\left | 8x-6\right |=3$

Possible Answers:

$x=0 \:or\:x=\frac{3}{2}$

$x=-3\:or\:x=1$

$x=\frac{3}{2}\:or\:x=10$

$x=\frac{3}{4}$

$x=-2\:or\:x=0$

Correct answer:

$x=0 \:or\:x=\frac{3}{2}$

Explanation:

To solve for first isolate the absolute value portion on one side of the equation and all other constants on the other side.

$-3-\left | 8x-6\right |=3$

$-\left | 8x-6\right |=6$

$\left | 8x-6\right |=-6$

Recall that the absolute value can come from either a negative or positive value therefore two possible equations are set up.

$8x-6=6\: \:or\: \:8x-6=-6$

$8x=12\: \:or\: \:8x=0$

$x=\frac{12}{8}=\frac{3}{2}\: \:or\: \:x=0$

Report an Error

Example Question #7 : Absolute Value Equations

Solve the equation:

$-5\left | 4+2x\right |=-100$

Possible Answers:

$x=0\:or\:x=-8$

$x=-8\:or\:x=9$

$x=-12\:or\:x=8$

$x=-\frac{1}{2}\:or\:x=4$

$x=-8\:or\:x=12$

Correct answer:

$x=-12\:or\:x=8$

Explanation:

To solve for first isolate the absolute value portion on one side of the equation and all other constants on the other side.

$-5\left | 4+2x\right |=-100$

$\left | 4+2x\right |=20$

Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.

$4+2x=20\: \:or\: \:4+2x=-20$

$2x=16\: \:or\: \:2x=-24$

$x=-12\:or\:x=8$

Report an Error

View College Algebra Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

View College Algebra Tutors

Zara
Certified Tutor

University of Manitoba, Bachelor in Arts, Mathematics.

View College Algebra Tutors

George
Certified Tutor

Pensacola State College, Bachelor in Arts, Mathematics.

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Miami, SSAT Tutors in Los Angeles, ISEE Tutors in San Francisco-Bay Area, Computer Science Tutors in Chicago, SSAT Tutors in Dallas Fort Worth, LSAT Tutors in Atlanta, ACT Tutors in Atlanta, Chemistry Tutors in Los Angeles, GMAT Tutors in Washington DC, Chemistry Tutors in Philadelphia

Popular Courses & Classes

SAT Courses & Classes in Denver, Spanish Courses & Classes in Houston, ISEE Courses & Classes in Chicago, GRE Courses & Classes in Chicago, ACT Courses & Classes in Miami, GRE Courses & Classes in Seattle, GRE Courses & Classes in Los Angeles, MCAT Courses & Classes in Miami, SSAT Courses & Classes in New York City, SAT Courses & Classes in Phoenix

Popular Test Prep

LSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Atlanta, ISEE Test Prep in Los Angeles, GRE Test Prep in Miami, SAT Test Prep in Los Angeles, MCAT Test Prep in Los Angeles, GRE Test Prep in Washington DC, GRE Test Prep in San Francisco-Bay Area, MCAT Test Prep in Houston, LSAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Absolute Value Equations

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #81 : Solving Equations And Inequallities

Example Question #82 : Solving Equations And Inequallities

Example Question #83 : Solving Equations And Inequallities

Example Question #84 : Solving Equations And Inequallities

Example Question #81 : Solving Equations And Inequallities

Example Question #4 : Absolute Value Equations

Example Question #85 : Solving Equations And Inequallities

Example Question #6 : Absolute Value Equations

Example Question #7 : Absolute Value Equations

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: