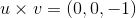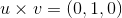We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 3 : Cross Product

Study concepts, example questions & explanations for Calculus 3

Create An Account

All Calculus 3 Resources

6 Diagnostic Tests 373 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Cross Product

Let u=(2,4,5) , and v=(-2,6,10) .

Find $u\times v$ .

Possible Answers:

$u\times v=(10,30,20)$

$u\times v=(40,-20,12)$

$u\times v=(-10,30,-20)$

$u\times v=(10,-30,20)$

$u\times v=(0,-3,2)$

Correct answer:

$u\times v=(10,-30,20)$

Explanation:

We are trying to find the cross product between and .

Recall the formula for cross product.

If u=(u_x,u_y,u_z) , and v=(v_x,v_y,v_z) , then

$u\times v=(u_yv_z-u_zv_y, -u_xv_z+u_zv_x, u_xv_y-u_yv_x)$ .

Now apply this to our situation.

$u\times v=(4(10)-5(6),-2(10)+5(-2), 2(6)-4(-2))$

$u\times v=(40-30,-20-10, 12+8)$

$u\times v=(10,-30,20)$

Report an Error

Example Question #2 : Cross Product

Let u=(1,0,1) , and v=(0,0,1) .

Find $u\times v$ .

Possible Answers:

$u\times v=(0,-1,0)$

$u\times v=(0,0,-1)$

$u\times v=(0,1,0)$

$u\times v=(0,0,0)$

$u\times v=(-1,0,0)$

Correct answer:

$u\times v=(0,-1,0)$

Explanation:

We are trying to find the cross product between and .

Recall the formula for cross product.

If u=(u_x,u_y,u_z) , and v=(v_x,v_y,v_z) , then

$u\times v=(u_yv_z-u_zv_y, -u_xv_z+u_zv_x, u_xv_y-u_yv_x)$ .

Now apply this to our situation.

$u\times v=(0(1)-1(0),-1(1)+1(0), 1(0)-0(0))$

$u\times v=(0-0,-1+0, 0-0)$

$u\times v=(0,-1,0)$

Report an Error

Example Question #3 : Cross Product

True or False: The cross product can only be taken of two 3-dimensional vectors.

Possible Answers:

False

True

Correct answer:

True

Explanation:

This is true. The cross product is defined this way. The dot product however can be taken for two vectors of dimension n (provided that both vectors are the same dimension).

Report an Error

Example Question #4 : Cross Product

Which of the following choices is true?

Possible Answers:

$\begin{matrix}\vec{A}\cdot \vec{B}=-\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= \vec{B}\times \vec{A} \end{matrix}$

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= \vec{B}\times \vec{A} \end{matrix}$

$\begin{matrix}\vec{A}\cdot \vec{B}=-\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$

Correct answer:

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$

Explanation:

By definition, the order of the dot product of two vectors does not matter, as the final output is a scalar. However, the cross product of two vectors will change signs depending on the order that they are crossed. Therefore

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$ .

Report an Error

Example Question #361 : Calculus 3

For what angle(s) is the cross product $\vec{A} \times \vec{B}=0$ ?

Possible Answers:

$30^{\circ}$

$270^{\circ}$

$90^{\circ}$

$0 ^{\circ}, 180 ^{\circ}, 360 ^{\circ}$

$45 ^{\circ}$

Correct answer:

$0 ^{\circ}, 180 ^{\circ}, 360 ^{\circ}$

Explanation:

We have the following equation that relates the cross product of two vectors $\vec{A} \times \vec{B}$ to the relative angle between them $\theta$ , written as

$\frac{\vec{A} \times \vec{B}}{\left| \vec{A} \right| \left| \vec{B} \right|}= \sin \theta$ .

From this, we can see that the numerator, or cross product, will be whenever $\sin \theta=0$ . This will be true for all even multiples of $\frac{\pi}{2}$ . Therefore, we find that the cross product of two vectors will be for $\theta = 0(0^{\circ}), \pi (180^{\circ}), 2\pi (360^{\circ})$ .

Report an Error

Example Question #1 : Cross Product

Evaluate $<1,0> \times <0,8>$

Possible Answers:

<0,0>

<0,8>

<0>

<0,0,0>

None of the other answers

Correct answer:

None of the other answers

Explanation:

It is not possible to take the cross product of -component vectors. The definition of the cross product states that the two vectors must each have components. So the above problem is impossible.

Report an Error

Example Question #7 : Cross Product

Compute $<1,0,4> \times <1,1,1>$ .

Possible Answers:

<3,4,-1>

<-3,-4,1>

<0,0,0>

<4,-3,-1>

<-4,3,1>

Correct answer:

<-4,3,1>

Explanation:

To evaluate the cross product, we use the determinant formula

$\mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1& a_2 & a_3 \\ b_1& b_2 & b_3 \end{vmatrix}$

So we have

$<1,0,4> \times <1,1,1>$

$= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1& 0 & 4 \\ 1& 1 & 1 \end{vmatrix}$

$= \begin{vmatrix} 0 & 4 \\ 1 & 1 \end{vmatrix} \mathbf{i} -\begin{vmatrix} 1 & 4 \\ 1& 1 \end{vmatrix} \mathbf{j} + \begin{vmatrix} 1 & 0 \\ 1 & 1 \end{vmatrix} \mathbf{k}$ . (Use cofactor expansion along the top row. This is typically done when taking any cross products)

$= -4\mathbf{i}-(-3)\mathbf{j}+1\mathbf{k}$

= <-4,3,1>

Report an Error

Example Question #1 : Cross Product

Evaluate $<1,1,0> \times <8,0,8>$ .

Possible Answers:

<1,1,-1>

<-8,8,8>

None of the other answers

<8,-8,-8>

<-1,-1,1>

Correct answer:

<8,-8,-8>

Explanation:

To evaluate the cross product, we use the determinant formula

$\mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1& a_2 & a_3 \\ b_1& b_2 & b_3 \end{vmatrix}$

So we have

$<1,1,0> \times <8,0,8>$

$= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1& 1 & 0 \\ 8& 0 & 8 \end{vmatrix}$

$= \begin{vmatrix} 1 & 0 \\ 0 & 8 \end{vmatrix} \mathbf{i} -\begin{vmatrix} 1 & 0 \\ 8& 8 \end{vmatrix} \mathbf{j} + \begin{vmatrix} 1 & 1 \\ 8 & 0 \end{vmatrix} \mathbf{k}$ . (Use cofactor expansion along the top row. This is typically done when taking any cross products)

$= 8\mathbf{i}-(8)\mathbf{j}+(-8)\mathbf{k}$

= <8,-8,-8>

Report an Error

Example Question #9 : Cross Product

Find the cross product of the two vectors.

u=<4,3,7>

v=<5,7,10>

Possible Answers:

<9,10,17>

<-19,-5,13>

<20,21,70>

<-1,-4,-3>

Correct answer:

<-19,-5,13>

Explanation:

To find the cross product, we solve for the determinant of the matrix

$\begin{vmatrix} i&j &k \\ 4&3 &7 \\ 5&7 &10 \end{vmatrix}$

The determinant equals

$=det(\begin{vmatrix} 3&7 \\ 7&10 \end{vmatrix})i-det(\begin{vmatrix} 4&7 \\ 5&10 \end{vmatrix})j+det(\begin{vmatrix} 4&3 \\ 5&7 \end{vmatrix})k$

=(3*10-7*7)i-(4*10-5*7)j+(4*7-5*3)k

=-19i-5j+13k

=<-19,-5,13>

As the cross-product.

Report an Error

Example Question #1 : Cross Product

Find the cross product of the two vectors.

u=<1,0,0>

v=<0,1,0>

Possible Answers:

<0,0,1>

<1,-1,0>

<1,1,0>

<0,0,0>

Correct answer:

<0,0,1>

Explanation:

To find the cross product, we solve for the determinant of the matrix

$\begin{vmatrix} i&j &k \\ 1&0 &0 \\ 0&1 &0 \end{vmatrix}$

The determinant equals

$=det(\begin{vmatrix} 0&0 \\ 1&0 \end{vmatrix})i-det(\begin{vmatrix} 1&0 \\ 0&0 \end{vmatrix})j+det(\begin{vmatrix} 1&0 \\ 0&1 \end{vmatrix})k$

=(0*0-1*0)i-(1*0-0*0)j+(1*1-0*0)k

=0i-0j+1k

=<0,0,1>

As the cross-product.

Report an Error

View Calculus 3 Tutors

George
Certified Tutor

Pensacola State College, Bachelor in Arts, Mathematics.

View Calculus 3 Tutors

Timothy
Certified Tutor

Bethune-Cookman University, Bachelor of Science, Mathematics. University of Phoenix, Master of Science, Computer and Informat...

View Calculus 3 Tutors

Evgenii
Certified Tutor

All Calculus 3 Resources

6 Diagnostic Tests 373 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in San Francisco-Bay Area, Calculus Tutors in Boston, Statistics Tutors in Chicago, Calculus Tutors in San Diego, English Tutors in Philadelphia, French Tutors in Philadelphia, Computer Science Tutors in Los Angeles, Spanish Tutors in Dallas Fort Worth, Computer Science Tutors in Philadelphia, GRE Tutors in Atlanta

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, ACT Courses & Classes in Philadelphia, SAT Courses & Classes in Denver, ISEE Courses & Classes in Chicago, MCAT Courses & Classes in Chicago, LSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Atlanta, GMAT Courses & Classes in Philadelphia, GRE Courses & Classes in Philadelphia, ISEE Courses & Classes in San Diego

Popular Test Prep

ACT Test Prep in Philadelphia, LSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Boston, LSAT Test Prep in Philadelphia, ACT Test Prep in Chicago, SAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in New York City, ISEE Test Prep in Atlanta, LSAT Test Prep in Washington DC, ISEE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 3 : Cross Product

Study concepts, example questions & explanations for Calculus 3

All Calculus 3 Resources

Example Questions

Example Question #1 : Cross Product

Example Question #2 : Cross Product

Example Question #3 : Cross Product

Example Question #4 : Cross Product

Example Question #361 : Calculus 3

Example Question #1 : Cross Product

Example Question #7 : Cross Product

Example Question #1 : Cross Product

Example Question #9 : Cross Product

Example Question #1 : Cross Product

All Calculus 3 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: