All Calculus 3 Resources
Example Questions
Example Question #591 : Calculus 3
Write the parametric equations of the line that passes through the points 

First, you must find the vector that is parallel to the line.
This vector is

From the points we were given, this becomes

To form the parametric equations, we need to pick a point that lies on the line we want.
The point 
The vector form of the line is from the following equation

We then rewrite each expression in terms of the variables x, y, and z.
Example Question #2 : Line Integrals
Evaluate the line integral 



Evaluate the line integral 

from

Define the Parametric Equations to Represent
The points given lie on the line 




_________________________________________________________________
The line integral of a function 





Where 


______________________________________________________________
Write the vector 
Differentiate,
The absolute value (magnitude) of this vector is:
Write the function 

Insert everything into Equation (1) noting that the limits of integration will be 



Example Question #1 : Arc Length And Curvature
Determine the length of the curve 
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Example Question #591 : Calculus 3
Determine the length of the curve 
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Example Question #1 : Arc Length And Curvature
Find the length of the curve 

None of the other answers
The formula for the length of a parametric curve in 3-dimensional space is
Taking dervatives and substituting, we have






![l = 2[\frac{1}{2}e^{2t}-\frac{1}{2}e^{-2t}]_{0}^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/616236/gif.latex)
Example Question #592 : Calculus 3
Find the length of the arc drawn out by the vector function 



None of the other answers
To find the arc length of a function, we use the formula

Using 
Example Question #4 : Arc Length And Curvature
Evaluate the curvature of the function 

The formula for curvature of a Cartesian equation is ![\kappa(x)= \frac{|f''(x)|}{[1+(f'(x))^2]^{3/2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679052/gif.latex)
We have 
and ![\kappa(1)= \frac{|20|}{[1+(20(1))^2]^{3/2}} = \frac{20}{401^{3/2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679055/gif.latex)
Example Question #3 : Arc Length And Curvature
Find the length of the parametric curve
for 
To find the solution, we need to evaluate

First, we find


So we have a final expression to integrate for our answer
Example Question #71 : 3 Dimensional Space
Determine the length of the curve given below on the interval 0<t<2
The length of a curve r is given by:
To solve:
Example Question #8 : Arc Length And Curvature
Find the arc length of the curve
on the interval
To find the arc length of the curve function
on the interval
we follow the formula
For the curve function in this problem we have
and following the arc length formula we solve for the integral
Hence the arc length is
Certified Tutor
All Calculus 3 Resources

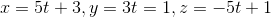


















![=\frac{\sqrt{41}}{4}\left[\frac{5}{8}t^2+\frac{1}{\pi}\sin(\pi t) \right ]_{t=0}^{t=4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933661/gif.latex)
![=\frac{\sqrt{41}}{4}\left[\frac{5}{8}(16)+\frac{1}{\pi }\sin(4 \pi) -0-\frac{1}{\pi}\sin(0)\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933662/gif.latex)











































![=[\sqrt2at]_0^\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/667563/gif.latex)






![\kappa(x)= \frac{|20|}{[1+(20x)^2]^{3/2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679054/gif.latex)








![\mathbf{r}=[2\sin t,\sqrt{5} t, 2\cos t]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/733160/gif.latex)

































