Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Derivatives

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #44 : New Concepts

Evaluate the following limit:

$\lim_{x\rightarrow 3} \frac{3-x}{x^2-9}$

Possible Answers:

$-\frac{1}{6}$

The limit does not exist

$\infty$

$\frac{1}{6}$

Correct answer:

$-\frac{1}{6}$

Explanation:

When we evaluate the limit using normal methods, we arrive at the indeterminate form $\frac{0}{0}$ . When this occurs, to evaluate the limit, we must use L'Hopital's Rule, which states that

$\lim_{x\rightarrow n}\frac{ f(x)}{g(x)}=\lim_{x\rightarrow n} \frac{f'(x)}{g'(x)}$

So, we must find the derivative of the top and bottom functions:

f'(x)=-1, g'(x)=2x

The derivatives were found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Now, rewrite the limit and evaluate it:

$\lim_{x\rightarrow 3}-\frac{1}{2x}=-\frac{1}{6}$

Report an Error

Example Question #23 : L'hospital's Rule

Evaluate the following limit:

$\lim_{x\rightarrow 2}\frac{x^2-4}{\sin(2-x)}$

Possible Answers:

$\infty$

Correct answer:

Explanation:

When we evaluate the limit using normal methods, we get the indeterminate form $\frac{0}{0}$ . When this happens, we must use L'Hopital's Rule, which states that $\lim_{x\rightarrow n}\frac{f(x)}{g(x)}=\lim_{x\rightarrow n}\frac{f'(x)}{g'(x)}$

Now, we must find the derivatives of the numerator and denominator:

$f'(x)=2x, g'(x)=-\cos(x-4)$

The derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} \sin(x)=\cos(x)$

Next, rewrite the limit and evaluate it:

$\lim_{x\rightarrow 2}\frac{2x}{-\cos(2-x)}=-4$

Report an Error

Example Question #24 : L'hospital's Rule

Use l'Hopital's rule to find the limit:

$\lim_{x \to 1} \frac{x^2-3x+2}{x-1}$

Possible Answers:

$\infty$

Correct answer:

Explanation:

The first thing we always have to do is to check that l'Hopital's rule is actually applicable when we want to use it.

$\frac{1^2-3\cdot1+2}{1-1} = \frac{0}{0}$

So it is applicable here.

We take the derivative of the top and bottom, and get

$\lim_{x \to 1} \frac{x^2-3x+2}{x-1} = \lim_{x \to 1} \frac{2x-3}{1}$

and now we can safely plug in x=1 and get that the limit equals

$2\cdot 1 -3 = -1$ .

Report an Error

Example Question #561 : Derivatives

Evaluate $\lim_{x \to 0^+} x\ln(x)$

Possible Answers:

Does not exist

$-\infty$

None of the other answers

Correct answer:

Explanation:

Plugging into the function $x\ln(x)$ head on yields the inteterminate form of zero times negative infinity, so we must rewrite the problem

$\lim_{x \to 0^+} x\ln(x)$ . Start

$=\lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x}}$

In this expression, when approaches from the positive side, the limit "approaches $-\frac{\infty}{\infty}$ " So we can use L'Hospital's rule.

$=\lim_{x \to 0} \frac{\frac{1}{x}}{-\frac{1}{x^2}}$

$=\lim_{x \to 0}-x$

Report an Error

Example Question #562 : Derivatives

Evaluate the following limit:

$\lim_{x\rightarrow 10} \frac{\cos(\frac{\pi x}{4})}{x-10}$

Possible Answers:

$\frac{\pi}{4}$

The limit does not exist

$-\frac{\pi}{4}$

Correct answer:

$-\frac{\pi}{4}$

Explanation:

When we evaluate the limit using normal methods, we get the indeterminate form $\frac{0}{0}$ .

So, we must use L'Hopital's Rule to evaluate the limit, which states that

$\lim_{x\rightarrow n} \frac{f(x)}{g(x)}=\lim_{x\rightarrow n}\frac{f'(x)}{g'(x)}$

Using the above, we get

$\lim_{x\rightarrow 10 } \frac{-\sin(\frac{\pi x}{4})(\frac{\pi}{4})}{1}=-\frac{\pi}{4}$

when we evaluate the limit using substitution.

Report an Error

Example Question #31 : L'hospital's Rule

$\lim_{x\rightarrow 0} \; \frac{sin(4x)}{2x}$

Possible Answers:

$\frac{1}{2}$

$\frac{1}{4}$

Correct answer:

Explanation:

If you plug in the limit value, the function turns into $\frac{0}{0}$ . Therefore, we are allowed to use l'Hospital's Rule. We start by taking the derivative of both the numerator and the denominator until when you plug in the value of the limit, you do not get something in the form $\frac{0}{0}$ . Luckily, in this case, we only need to take the derivative once. By taking the derivatives separately, we get a new limit:

$\lim_{x\rightarrow 0} \frac{4cos(4x)}{2}=\frac{4cos(0)}{2}=\frac{4}{2}=2$ .

Report an Error

Example Question #561 : Derivatives

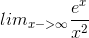
Evaluate: $lim_{x->\infty} \frac{e^x}{x^2}$

Possible Answers:

e^x

$\infty$

Limit Does Not Exist

Correct answer:

$\infty$

Explanation:

Report an Error

Example Question #33 : L'hospital's Rule

Find the limit using L'Hospital's Rule.

$\lim_{x \to \infty}xe^{-x}$

Possible Answers:

DNE

$\infty$

Correct answer:

Explanation:

We rewrite the limit as

$\lim_{x\to\infty}\frac{x}{e^x}$

Substituting $x=\infty$ yields the indeterminate form

$\frac{\infty}{\infty}$

L'Hospital's Rule states that when the limit is in indeterminate form, the limit becomes

$\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}$

For f(x)=x and g(x)=e^x we solve the limit

$\lim_{x\to\infty}\frac{1}{e^x}$

and substituting $x=\infty$ we find that

$\lim_{x\to\infty}\frac{1}{e^x}=\frac{1}{\infty}=0$

As such

$\lim_{x \to \infty}xe^{-x}=0$

Report an Error

Example Question #34 : L'hospital's Rule

Find the limit using L'Hospital's Rule.

$\lim_{x \to \infty}\frac{ln\,x}{x}$

Possible Answers:

DNE

$\infty$

Correct answer:

Explanation:

Substituting $x=\infty$ yields the indeterminate form

$\frac{\infty}{\infty}$

L'Hospital's Rule states that when the limit is in indeterminate form, the limit becomes

$\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}$

For $f(x)=ln\,x$ and g(x)=x we solve the limit

$\lim_{x\to\infty}\frac{\frac{1}{x}}{1}$

and substituting $x=\infty$ we find that

$\lim_{x\to\infty}\frac{\frac{1}{x}}{1}=\frac{1}{\infty}=0$

As such

$\lim_{x \to \infty}\frac{ln\,x}{x}=0$

Report an Error

Example Question #35 : L'hospital's Rule

Evaluate the following limit:

$\lim_{x \to 0} \frac{6^x-8^x}{x}$

Possible Answers:

$ln(\frac{3}{4})$

ln(12)

$\infty$

Correct answer:

$ln(\frac{3}{4})$

Explanation:

Simply substituting x=0 in the given limit will not work:

$\lim_{x \to 0} \frac{6^x-8^x}{x} = \frac{6^0-8^0}{0}$

$= \frac{1-1}{0}$

$= \frac{0}{0}$

Because direct substitution yields an indeterminate result, we must apply L'Hospital's rule to the limit:

$\lim_{x \to a}\frac{f(x)}{g(x)} = \lim_{x \to a}\frac{f'(x)}{g'(x)}$

if and only if $g'(x)\neq 0$ and both f'(x) and g'(x) exist at .

Here,

f'(x) = ln(6)6^x-ln(8)8^x, and g'(x)=1 .

Hence,

$\lim_{x \to 0}\frac{6^x-8^x}{x}=\lim_{x \to 0}\frac{ln(6)6^x-ln(8)8^x}{1}$

$= \lim_{x \to 0}(ln(6)6^x-ln(8)8^x)$

= ln(6)6^0-ln(8)8^0

= ln(6)-ln(8)

$= ln(\frac{3}{4})$

Report an Error

View Calculus 2 Tutors

Anabel
Certified Tutor

UDELAR, Diploma, Chemistry. IPA, Bachelor of Education, Mathematics.

View Calculus 2 Tutors

Gary
Certified Tutor

SUNY at Albany, Bachelor of Science, Economics. Pace University-New York, Masters in Business Administration, Analysis and Fu...

View Calculus 2 Tutors

Muhammad
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Mechanical Engineering.

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Boston, LSAT Tutors in Atlanta, Spanish Tutors in New York City, SAT Tutors in Chicago, Statistics Tutors in Seattle, Physics Tutors in Boston, MCAT Tutors in Boston, GRE Tutors in Miami, LSAT Tutors in Denver, Computer Science Tutors in San Diego

Popular Courses & Classes

Spanish Courses & Classes in Seattle, SSAT Courses & Classes in Denver, ACT Courses & Classes in Houston, ISEE Courses & Classes in Houston, MCAT Courses & Classes in Chicago, Spanish Courses & Classes in Philadelphia, SSAT Courses & Classes in Chicago, SAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Chicago, SAT Courses & Classes in Houston

Popular Test Prep

ISEE Test Prep in Houston, LSAT Test Prep in Los Angeles, SAT Test Prep in Denver, MCAT Test Prep in Houston, SSAT Test Prep in Washington DC, LSAT Test Prep in New York City, SSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Atlanta, LSAT Test Prep in Chicago, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Derivatives

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #44 : New Concepts

Example Question #23 : L'hospital's Rule

Example Question #24 : L'hospital's Rule

Example Question #561 : Derivatives

Example Question #562 : Derivatives

Example Question #31 : L'hospital's Rule

Example Question #561 : Derivatives

Evaluate: $lim_{x->\infty} \frac{e^x}{x^2}$

Example Question #33 : L'hospital's Rule

Example Question #34 : L'hospital's Rule

Example Question #35 : L'hospital's Rule

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: