All Calculus 2 Resources
Example Questions
Example Question #252 : First And Second Derivatives Of Functions
Find the second derivative of 
Before finding the second derivative, you must find the first derivative. Remember to multiply the exponent by the coefficient and then subtract one from the exponent. Evaluate each term separately and then put all together at the end.
The first derivative is: 
Now, take the derivative of the 1st derivative to find the second derivative:

Example Question #253 : First And Second Derivatives Of Functions
Find the first derivative of 
First, chop up the fraction into 2 separate terms and simplify:
Now, take the derivative of that expression. Remember to multiply the exponent by the coefficient and then decrease the exponent by 1:
Example Question #251 : First And Second Derivatives Of Functions
Integrate each term separately. When there is just an x on the denominator, the integral of that is 
Therefore, the first term integrated is:
The second term integrated is:
Put those together to get:
Because it's an indefinite integral, remember to add C at the end:

Example Question #181 : Derivatives
Given the velocity function
where 
![d\in [0,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600903/gif.latex)

We can find the acceleration function 
We can view the function
as the composition of the following functions
so that 
to find the derivative. We have 

Example Question #1581 : Calculus Ii
Define 
Find 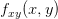
First, find 
Therefore,
Now, find 
Example Question #1582 : Calculus Ii
Consider the equation
where 

Which of the following is equal to 
Example Question #1 : Other Derivative Review
Use implicit differentiation to find 
To differentiate the left-hand side of the equation, we must use the product rule: 
Let 




Using algebra to isolate the 

Example Question #2 : Other Derivative Review
Find 
Since 
Differentiating the latter equation, we obtain 
Thus, 
Example Question #461 : Derivative Review
Define 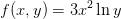
Find 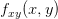
First, find 
Therefore, 
Now, find 
Example Question #1583 : Calculus Ii
Define 
Find 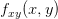
First, find 
Therefore, 
Now, find 
All Calculus 2 Resources
































![[g(h(x))]'=g'(h(x))h'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600919/gif.latex)
![a(x)=v'(x)=[(x+1)^2]^d\sin [(x+1)^2]^5\cdot (2x+2)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600925/gif.latex)















































































