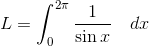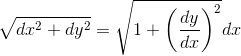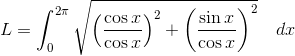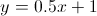All Calculus 1 Resources
Example Questions
Example Question #1 : How To Find Length Of Line By Graphing Functions
Consider a function 

Which integral can calculate the length along this curve between 

This is not possible with the information given.
To determine the length of a curve between two points, we evaluate the integral
There are many reasons this works, but we'll give an informal explanation here:
If we divide this curve into three line-segments, we can see that they become more and more similar to the original curve. By adding up all the little hypotenuses, we can arrive at the length of the curve. Note, that
If we think of the integration symbol as a sum of infinitely small parts, this gets us the formula for length:

Returning to the problem, we plug the derivative into the length formula:
substitute:
Simplify:
By trigonometric identities we get:
Example Question #2 : How To Find Length Of Line By Graphing Functions
Find the length of the line segment between points A and B:
The distance between two points can be easily found using the Distance Formula:
Applying the points we are given to this formula results in:
This is one of the answer choices.
Example Question #1 : Lines
What is the equation of the line tangent to f(x) = 4x3 – 2x2 + 4 at x = 5?
None of the other answers
y = 280x – 946
y = 85x + 24
y = 44x + 245
y = 220x – 550
y = 280x – 946
First, take the derivative of f(x). This is very easy:
f'(x) = 12x2 – 4x
Now, the slope of the tangent line at x = 5 is f'(5). Evaluated, this is: f'(5) = 12 * 5 * 5 – 4 * 5 = 300 – 20 = 280
Now, we must find the intersection point on the original line:
f(5) = 4 * 53 – 2 * 52 + 4 = 500 – 50 + 4 = 454
Therefore, the point of tangent intersection is (5,454).
Using the point-slope form of linear equations, we can find the line:
(y – 454) = 280(x – 5)
y – 454 = 280x – 1400
y = 280x – 946
Example Question #2 : Lines
Find the equation of the line tangent to 

The equation of the tangent line will have the form 


To find the slope, we need to evaluate the derivative at 

Now that we have the slope, we can determine the equation of the tangent line using the point-slope formula:
Example Question #2 : Equation Of Line
Find the equation of the line tangent to 

To find the equation of the line at that point, you need two things: the slope at that point and the y adjustment of the function, in the form 





To find the y adjustment pick a point 0 in the original



Now you simply solve for 

Final equation of the line tangent to 

Example Question #3 : Lines
Find the equation of the line tangent to 

To get the slope, find the derivative of 



Remember that the derivative of 
To find the 







The coefficient in front of the 
Now you simply solve for 

Final equation of the line tangent to 


Example Question #4 : Lines
Find the equation of the line tangent to 


The equation of the tangent line is 

The next step is to choose a coordinate on the original 


Let's choose 
The 

Plugging in those values we can solve for 
Solving for 


Example Question #3 : How To Find Equation Of Line By Graphing Functions
A function, 

Find the line tangent to 

First we need to find the slope of 


At,
Now we need to know

Now we have a slope, 
so we can use the point-slope formula to find the equation of the line.
Plugging in and rearranging we find

Example Question #1 : Lines
Let 
Find the equation for a line tangent to 

First, evaluate 

Thus, we need a line that contains the point
Next, find the derivative of 

To find the derivative we will use the power rule,

This indicates that we need a line with a slope of 8.
In point-slope form, 

Example Question #4 : How To Find Equation Of Line By Graphing Functions
What is the equation of the line tangent to 

The tangent line to 


Applying the chain rule we get

Therefore the slope of the line is,

In addition, the tangent line touches the graph of 



Plugging in the slope and point we get 
Certified Tutor
All Calculus 1 Resources