All Calculus 1 Resources
Example Questions
Example Question #2 : How To Write Equations
Find the equation tangent to 
Equation of tangent line is undefined
First, find the y coordinate of the function at
Thus, we have the point 
To find the slope of the tangent line, take the derivative and then plug in
Thus, our slope is 
Knowing that the general formula of a straight line is 






So now the equation of the tangent line becomes
Example Question #1 : How To Write Equations
Take the indefinite integral of
Indefinite integral does not exist
First, foil the integral so it is easier to manage.
then perform the indefinite integral the normal way you would do
Example Question #1 : How To Write Equations
Find the limit of 
In this limit, we have 

Because of this, we can use L'Hospital's rule. Differentiating the top and the bottom of the function, we get

If we evaluate at 


So the answer is 2.
Example Question #4 : How To Write Equations
Find
Because we have a 

Evaluating this as 
Example Question #1 : How To Write Equations
What is the equation of the tangent line at x = 15 for f(x) = x4 + 5x2 + 44x – 3?
y = 55x + 13382
y = 2848x + 34
y = 153103x – 13694
y = 13694x – 153003
None of the other answers
y = 13694x – 153003
First we must solve for the general derivative of f(x) = f(x) = x4 + 5x2 + 44x – 3.
f'(x) = 4x3 + 10x + 44
Now, the slope of the tangent line for f(15) is equal to f'(15):
f'(15) = 4(15)3 + 10 *15 + 44 = 13694.
To find the tangent line, we need at least one point on the line. To find this, we can use f(15) to get the y value of the point of tangency, which will suffice for our use:
f(15) = 154 + 5(15)2 + 44 * 15 – 3 = 50625 + 1125 + 660 – 3 = 52407
Now, using the point-slope form of the line, we get:
y - 52407 = 13694 * (x – 15)
Simplify:
y – 52407 = 13694x – 205410
y = 13694x – 153003
Example Question #8 : How To Write Equations
For the following function, use implicit differentiation to find the equation of the tangent line at 
Our first step is to apply implicit differentiation to the function to find y’. This derivative tells us the slope of our function and will therefore give us the slope of our tangent line at the given point:
Rearranging the equation, factoring out y’, and dividing, we find y’ is:
Before we can plug in the values of our given point to find the slope of the tangent line, we must first find its y value by plugging x=0 into the original function, which gives us:
So now that we know our given point is (0,3), we plug these values into our equation for y’, which gives us the slope of the tangent line at that point.
Now that we have our slope (m), an x coordinate (x1), and a y coordinate (y1), we can simply plug these values into the point-slope formula for a line:
Example Question #5 : How To Write Equations
Find two positive numbers whose sum is 
This problem deals with the concept of optimization. We start by simply writing out the equations described in words by the problem:
The problem asks that we maximize the product of the two unknown numbers, C, but we must first solve our first equation for y. Then we substitute it into our second equation to ensure that it is in terms of x alone. We then take the derivative of the equation with respect to x, and set it equal to 0 to solve for the x value that corresponds to the critical point of the function:
Because we only know that this x value corresponds to a critical point, and not necessarily whether that point is a minimum or a maximum, we must check the value of the second derivative at this point to see whether the function is concave up or concave down:
Because the value of the second derivative at this point is negative, we know that the function is concave down, so our one and only critical point in this case occurs at a global maximum, verifying that the product of the two numbers is maximized when x=225. Now that we know the value of x, we substitute it into the equation for y to find our second unknown number:
Example Question #10 : How To Write Equations
What is the equation of a line with slope of 


To write this equation we need to read the question carefully. Since the slope is we know the slope is represented by

Also since the y-intercept is 



Therefore plugging our values into the slope intercept form:


Example Question #11 : Other Writing Equations
My friend has 






My friend starts off with 

So, we need an equation that reflects that she has 

Example Question #12 : Other Writing Equations
Identify the inner and the outer functions of the following equation (let 

The first section of the equation to be resolved (in this case 1-4x) is the innermost function and the second section to solve is the outer function. So:
becuase g(x) must be performed first before plugging it into f(x).
All Calculus 1 Resources

















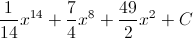






















































![y=\sqrt[3]{1-4x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370099/gif.latex)

![g(x)=\sqrt[3]{1-4x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370090/gif.latex)
![f(x)=\sqrt[3]{1-4x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370087/gif.latex)

![f(x)=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370085/gif.latex)

![g(x)=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370091/gif.latex)

![f(x)=\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370100/gif.latex)




