Basic Geometry : Right Triangles
Study concepts, example questions & explanations for Basic Geometry
All Basic Geometry Resources
Example Questions
Example Question #14 : How To Find The Height Of A Right Triangle
If the area of a right triangle is 
Recall how to find the area of a right triangle:
Now, we are going to manipulate the equation to solve for height.
Now, plug in the information given by the question about the values of the area and base of the triangle to find the height.
Example Question #15 : How To Find The Height Of A Right Triangle
If the area of a right triangle is 
Recall how to find the area of a right triangle:
Now, we are going to manipulate the equation to solve for height.
Now, plug in the information given by the question about the values of the area and base of the triangle to find the height.
Example Question #16 : How To Find The Height Of A Right Triangle
Find the missing length in triangle ABC.
To find the missing length, use the Pythagorean Theorem.
Where "a" and "b" are the legs, and "c" is the hypotenuse.
a=3 inches
b=???
c= 5 inches
Plug in the values
Now, get the variable by itself.
Take the square root of both sides.
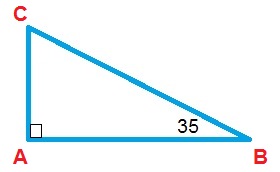
Example Question #1 : How To Find An Angle In A Right Triangle
Find angle C.
C=72
None of these
C=53
C=70
C=65
C=65
First, know that all the angles in a triangle add up to 180 degrees.
Each triangle has 3 angles. Thus, we have the sum of three angles as shown:
where we have angles A, B, and C. In our right triangle, one angle is 25 degree and we'll call that angle A. The other known angle is 90 degrees and we'll call this angle B. Thus, we have
Simplify and solve for C.
Example Question #1 : How To Find An Angle In A Right Triangle
Which of the following can be two angle measures of a right triangle?
A right triangle cannot have an obtuse angle; this eliminates the choice of 100 and 10.
The acute angles of a right triangle must total 90 degrees. Three choices can be eliminated by this criterion:
The remaining choice is correct:
Example Question #1 : How To Find An Angle In A Right Triangle
A right triangle has an angle that is 15 more than twice the other. What is the smaller angle?
The sum of the angles in a triangle is 180. A right triangle has one angle of 90. Thus, the sum of the other two angles will be 90.
Let 
So the equation to solve becomes 
Thus, the first angle is 
So the smaller angle is
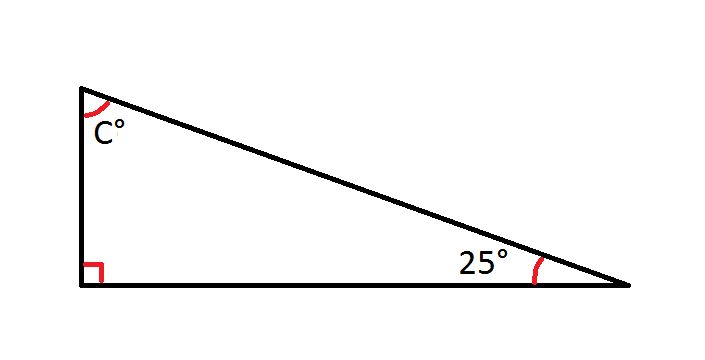
Example Question #1 : How To Find An Angle In A Right Triangle
Angle 
The interior angles of a triangle always add up to 180 degrees. We are given angle 
Angle 
Example Question #3 : How To Find An Angle In A Right Triangle
Which of the following cannot be true of a right triangle?
The measures of the angles of a right triangle can total 
One leg can be longer than the hypotenuse.
A right triangle can be equilateral.
A right triangle can have an obtuse angle.
None of the other statements can be true of a right triangle.
None of the other statements can be true of a right triangle.
All of these statements are false.
A right triangle can be equilateral.
False: An equilateral triangle must have three angles that measure 
One leg can be longer than the hypotenuse.
False: Each leg is shorter than the hypotenuse.
A right triangle can have an obtuse angle.
False: Both angles of a right triangle that are not right must be acute.
The measures of the angles of a right triangle can total 
False: The measures of any triangle total 
Example Question #1 : How To Find An Angle In A Right Triangle
In triangle 
The formula to find all the angles of a triangle is:
To solve for the measure of angle 
Example Question #1 : How To Find An Angle In A Right Triangle
Find the degree measure of the missing angle.
All the angles in a triangle add up to 180º.
To find the value of the remaining angle, subtract the known angles from 180º:
Therefore, the third angle measures 43º.
All Basic Geometry Resources
