We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Basic Geometry : Right Triangles

Study concepts, example questions & explanations for Basic Geometry

Create An Account

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 … 35 36 Next →

Example Question #201 : Triangles

Triangles 3

Refer to the above diagram.

True or false: $\bigtriangleup AOB \sim \bigtriangleup COD$

Possible Answers:

True

False

Correct answer:

True

Explanation:

The distance from the origin to A (0, 12) is the absolute value of the -coordinate of , which is OA = 12 . Similarly, OB = 6 , OC = 16 , and OD = 8 . Also, since the axes intersect at right angles, $\angle AOB$ and $\angle COD$ are both right, and, consequently, congruent.

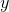
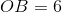
According to the Side-Angle-Side Similarity Theorem (SASS), if two sides of a triangle are in proportion to the corresponding sides of a second triangle, and their included angles are congruent, the triangles are similar.

We can test the proportion statement

$\frac{OA}{OC} = \frac{OB}{OD}$

by substituting:

$\frac{12}{16} = \frac{6}{8}$

Test the truth of this statement by comparing their cross products:

$12 \times 8 = 6 \times 16$

96 = 96

The cross-products are equal, making the proportion statement true, so two pairs of sides are in proportion. Also, their included angles $\angle AOB$ and $\angle COD$ are congruent. This sets up the conditions of SASS, so $\bigtriangleup AOB \sim \bigtriangleup COD$ .

Report an Error

Example Question #1181 : Basic Geometry

Triangles

Refer to the above figure.

True, false, or inconclusive: $\bigtriangleup ADB \sim \bigtriangleup BDC$ .

Possible Answers:

Inconclusive

False

True

Correct answer:

True

Explanation:

$\overline{AD}$ is an altitude of $\bigtriangleup ABC$ , so it divides the triangle into two smaller triangles similar to each other - that is, if we match the shorter legs, the longer legs, and the hypotenuses, the similarity statement is

$\bigtriangleup ADB \sim \bigtriangleup BDC$ .

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

What is the length of the remaining side of the right triangle?

Possible Answers:

$7\ cm$

$14\ cm$

$10\ cm$

$12\ cm$

$6\ cm$

Correct answer:

$12\ cm$

Explanation:

Rearrange the Pythagorean Theorem to find the missing side. The Pythagorean Theorem is:

$c^{2}=a^{2}+b^{2}$

where is the hypotenuse and and are the sides.

$\sqrt{(15^{2}-9^{2})} = 12$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

The hypotenuse of a right triangle is 26 in and one leg is 10 in. What is the sum of the two shortest sides?

Possible Answers:

$36\; in$

$30\; in$

$32\; in$

$34\; in$

$28\; in$

Correct answer:

$34\; in$

Explanation:

We use the Pythagorean Theorem so the problem to solve becomes $10^{2}+x^{2}=26^{2}$ where = unknown leg length

So $100 + x^{2}=676$ and $x=24\; in$

The sum of the two legs becomes $10+24=34\; in$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

$In\;\Delta KLM,\;what\;is\;the\;length\;of\;\overline{KL}?$

Possible Answers:

Correct answer:

Explanation:

$Use\;the\;Pythagorean\;Theorem: A^2+B^2=C^2$

$\fn_cm A^2+4^2=5^2$

A^2+16=25

A^2=25-16=9

$A=\sqrt9$

A=3

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Find the length of the unknown side, , of the right triangle below.

Triangle_a_9_12

Possible Answers:

$2\sqrt7$

$3\sqrt7$

$3\sqrt{10}$

$2\sqrt{5}$

$3\sqrt5$

Correct answer:

$3\sqrt7$

Explanation:

We need to use the Pythagorean Theorem, which says that a^2+b^2=c^2 .

Since we need to find the length of 'a', we can just solve for 'a'.

a^2=c^2-b^2

$a=\sqrt{c^2-b^2}$

In our case, c = 12 and b = 9.

Thus, $a=\sqrt{12^2-9^2}=\sqrt{144-81}=\sqrt{63}=\sqrt{9 \cdot 7}=\sqrt{9}\sqrt{7}=3\sqrt7$ .

Report an Error

Example Question #3 : How To Find The Length Of The Side Of A Right Triangle

Find the missing leg of the right triangle when one of the legs is and the hypotenuse is .

Possible Answers:

Correct answer:

Explanation:

In order to find the missing side of a right triangle you must use one of two things:

1. Pythagorean Theorem

2. Trigonometry.

Since we only know what the side lengths are we must use the Pythagorean Theorem.

a^2 +b^2 =c^2

a=4, b=x, and c=5

(4)^2+x^2=(5)^2

16+x^2=25

x^2=9

x=3

So the missing side length is 3

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Given that the hypotenuse of a right triangle is and one side is , find the other side length.

Possible Answers:

144

Correct answer:

Explanation:

To find the length of the missing side, you can either use the pythagorean theorm or realize this is a case of a special right triangle with sides 5,12,13 .

Thus, the other side length is .

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Find the length of the missing side.

Possible Answers:

20.49

21.65

22.39

19.61

Correct answer:

20.49

Explanation:

Recall the Pythagorean Theorem for a right triangle:

a^2+b^2=c^2

Since the missing side corresponds to side , rewrite the Pythagorean Theorem and solve for .

b^2=c^2-a^2

$b=\sqrt{c^2-a^2}$

Now, plug in values of and into a calculator to find the length of side . Round to decimal places.

$b=\sqrt{22^2-8^2}=\sqrt{420}=20.49$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Find the length of the missing side.

Possible Answers:

18.01

20.07

21.97

16.37

Correct answer:

20.07

Explanation:

Recall the Pythagorean Theorem for a right triangle:

a^2+b^2=c^2

Since the missing side corresponds to side , rewrite the Pythagorean Theorem and solve for .

b^2=c^2-a^2

$b=\sqrt{c^2-a^2}$

Now, plug in values of and into a calculator to find the length of side . Round to decimal places.

$b=\sqrt{22^2-p^2}=\sqrt{403}=20.07$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 … 35 36 Next →

View Tutors

Richard
Certified Tutor

Rutgers University-Newark, Bachelor of Science, Chemistry. Rutgers University-Newark, Doctor of Science, Chemistry.

View Tutors

Nazia
Certified Tutor

Osmania University, Bachelor of Science, Mathematics.

View Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in San Diego, Calculus Tutors in Los Angeles, SAT Tutors in Miami, SAT Tutors in Chicago, Math Tutors in New York City, Calculus Tutors in San Francisco-Bay Area, Computer Science Tutors in Washington DC, SSAT Tutors in San Francisco-Bay Area, English Tutors in Chicago, Chemistry Tutors in Chicago

Popular Courses & Classes

GRE Courses & Classes in Washington DC, ISEE Courses & Classes in Phoenix, GMAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in Miami, LSAT Courses & Classes in San Diego, GMAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Houston, ACT Courses & Classes in New York City, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in Seattle, SAT Test Prep in San Diego, GMAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Philadelphia, ACT Test Prep in Dallas Fort Worth, GRE Test Prep in Chicago, SSAT Test Prep in Houston, LSAT Test Prep in San Diego, SAT Test Prep in Atlanta, LSAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Basic Geometry : Right Triangles

Study concepts, example questions & explanations for Basic Geometry

All Basic Geometry Resources

Example Questions

Example Question #201 : Triangles

Example Question #1181 : Basic Geometry

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #3 : How To Find The Length Of The Side Of A Right Triangle

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

All Basic Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: