All Basic Geometry Resources
Example Questions
Example Question #1541 : Plane Geometry

Refer to the above figure.
True or false: 

False
True
False
Two rays are opposite rays, by definition, if
(1) they have the same endpoint, and
(2) their union is a line.
The first letter in the name of a ray always refers to the endpoint of the ray. Therefore, 



Example Question #1542 : Basic Geometry

Refer to the above figure.
True or false: 

False
True
False
The first letter in the name of a ray refers to its endpoint; the second refers to the name of any other point on the ray. 





As it turns out, the two rays are one and the same.
Example Question #691 : Geometry

Refer to the above figure.
True or false: 

False
True
True
Two rays are opposite rays, by definition, if
(1) they have the same endpoint, and
(2) their union is a line.
The first letter in the name of a ray refers to its endpoint; the second refers to the name of any other point on the ray. 









The union of the two rays is a line. Both criteria are met, so the rays are indeed opposite.
Example Question #11 : How To Find A Ray

Refer to the above diagram.
True or false: 


True
False
False
Three points are collinear if there is a single line that passes through all three. In the diagram below, it can be seen that the line that passes through 



Therefore, the three points are not collinear.
Example Question #13 : Lines

Refer to the above diagram.
True or false: 


False
True
True
Three points are collinear if there is a single line that passes through all three. In the diagram below, it can be seen that such a line exists.

Example Question #1546 : Basic Geometry

True or false: The plane containing the above figure can be called Plane 
False
True
True
A plane can be named after any three points on the plane that are not on the same line. 






Plane 
Example Question #1541 : Plane Geometry

Refer to the above diagram.
True or false: Quadrilateral 

False
True
False
A quadrilateral is named after its four vertices in consecutive order, going clockwise or counterclockwise. Quadrilateral 






Example Question #1541 : Plane Geometry

Refer to the above diagram:
True or false: 

True
False
False
A line can be named after any two points it passes through. The line 

The line does not pass through 


Example Question #1 : How To Find An Angle Of A Line

Examine the diagram. Which of these conditions does not prove that 


Any of these statements can be used to prove that 
If 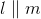
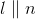

If 


If 


However, 


Example Question #1542 : Plane Geometry
An isosceles triangle has an interior angle that measures 
This triangle cannot exist.
By the Isosceles Triangle Theorem, two interior angles must be congruent. However, since a triangle cannot have two obtuse interior angles, the two missing angles must be the ones that are congruent. Since the total angle measure of a triangle is 

Certified Tutor
Certified Tutor
All Basic Geometry Resources











