All AP Statistics Resources
Example Questions
Example Question #1 : Bivariate Data
In a regression analysis, the y-variable should be the ___________ variable, and the x-variable should be the ___________ variable.
Greater, Lesser
First, Second
Qualified, Unqualified
Independent, Dependent
Dependent, Independent
Dependent, Independent
Regression tests seek to determine one variable's ability to predict another variable. In this analysis, one variable is dependent (the one predicted), and the other is independent (the variable that predicts). Therefore, the dependent variable is the y-variable and the independent variable is the x-variable.
Example Question #2 : Bivariate Data
If a data set has a perfect negative linear correlation, has a slope of 

The key here is to utilize

"Perfect negative linear correlation" means 



Example Question #2 : Bivariate Data
A least-squares regression line has equation 


Use the formula 
Plug in the given values for 

Example Question #1 : How To Find Outliers
Use the following five number summary to determine if there are any outliers in the data set:
Minimum:
Q1:
Median:
Q3:
Maximum:
There is at least one outlier on the high end of the distribution and at least one outlier on the low end of the distribution.
There is at least one outlier on the low end of the distribution and no outliers on the high end of the distribution.
There are no outliers.
It is not possible to determine if there are outliers based on the information given.
There is at least one outlier on the high end of the distribution and no outliers on the low end of the distribution.
There are no outliers.
An observation is an outlier if it falls more than 





Example Question #2 : How To Find Outliers
For a data set, the first quartile is 


Based on this information, a new observation can be considered an outlier if it is greater than what?
Use the 
This states that anything less than 

Thus, we want to find


Therefore, any new observation greater than 115 can be considered an outlier.
Example Question #1 : How To Find Outliers
You are given the following information regarding a particular data set:
Q1:
Q3:
Assume that the numbers 

Two
None of the numbers are outliers
Four
One
Three
Two
In order to find the outliers, we can use the 

Only two numbers are outside of the calculated range and therefore are outliers: 

Example Question #4 : How To Find Outliers
Use the following five number summary to answer the question below:
Min:
Q1:
Med:
Q3:
Max:
Which of the following is true regarding outliers?
There are no outliers in the upper side of the data set, but there is at least one outlier on the lower side of the data set.
There are no outliers in this data set.
There are no outliers in the lower side of the data set, but there is at least one outlier on the upper side of the data set.
There is at least one outlier in the lower side of the data set and at least one outlier in the upper side of the data set.
There is only one outlier in this entire data set.
There is at least one outlier in the lower side of the data set and at least one outlier in the upper side of the data set.
Using the 

This allows us to determine that there is at least one outlier in the upper side of the data set and at least one outlier in the lower side of the data set. Without any more information, we are not able to determine the exact number of outliers in the entire data set.
Example Question #5 : How To Find Outliers
Which values in the above data set are outliers?
no outliers
Step 1: Recall the definition of an outlier as any value in a data set that is greater than 

Step 2: Calculate the IQR, which is the third quartile minus the first quartile, or 










Step 3: 

Example Question #1 : How To Find Outliers
A certain distribution has a 1st quartile of 8 and a 3rd quartile of 16. Which of the following data points would be considered an outlier?
An outlier is any data point that falls 





Example Question #271 : Ap Statistics
On a residual plot, the 

independent variable;
independent variable; the dependent variable
dependent variable; residuals
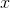

residuals; the independent variable
independent variable;
A residual plot shows the difference between the actual and expected value, or residual. This goes on the y-axis. The plot shows these residuals in relation to the independent variable.
All AP Statistics Resources



























































