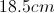All AP Physics C: Mechanics Resources
Example Questions
Example Question #11 : Calculating Electric Potential

A thin bar of length L lies in the xy plane and carries linear charge density 



Use the linear charge density 



Example Question #32 : Electricity And Magnetism Exam

A uniformly charged ring of radius 


Use the linear charge density 





Example Question #33 : Electricity And Magnetism Exam

A uniformly charged square frame of side length 

You may wish to use the integral:
Calculate the potential due to one side of the bar, and then multiply this by 


Example Question #31 : Electricity
Consider a spherical shell with radius 

Zero
Zero
According to the shell theorem, the total electric field at the center point of a charged spherical shell is always zero. At this point, any electric field lines will result in symmetry, canceling each other out and creating a net field of zero at that point.
Example Question #34 : Electricity And Magnetism Exam
A charge of unknown value is held in place far from other charges. Its electric field lines and some lines of electric equipotential (V1 and V2) are shown in the diagram.

A second point charge, known to be negative, is placed at point A in the diagram. In which direction will the second, negative charge freely move?
Toward point C
It will remain stationary
Toward the original charge Q
Toward point A
Toward point C
The original charge Q is negative, as indicated by the direction of the electric field lines in the diagram. A negative point charge of any value placed at point A will cause both charges to feel a mutually repelling force on each other. Therefore, the second charge will be repelled by the original negative charge with a force pointing radially along a line connecting the center of Q and the point A, resulting in free movement toward C. Additionally, point B is on a line of equipotential to point A; negative point charges will move from regions of lower electric potential to higher electric potential (against the direction of the electric field lines), so point B is not a viable answer.
Example Question #35 : Electricity And Magnetism Exam
A proton traveling 


To calculate the magnetic force of a single charge, we use 



Since this magnetic force causes the proton to travel in a circular path, we set this magnetic force equation equal to the centripetal force equation.



Using the values given in the question, we can solve for the radius.
Example Question #31 : Electricity And Magnetism Exam
Which of the following best describes the net magnetic flux through a closed sphere, in the presence of a magnet?
Zero only if the magnet is completely enclosed within the surface
Zero regardless of the orientation of the magnet
Negative only if the north pole of the magnet is within the surface
Positive only if the north pole of the magnet is within the surface
More than one of the other options is true
Zero regardless of the orientation of the magnet
The net magnetic flux (or net field flowing in and out) through any closed surface must always be zero. This is because magnetic field lines have no starting or ending points, so any field line going into the surface must also come out. In other words, "there are no magnetic monopoles."
Example Question #1 : Magnetism
A particle of charge 



Relevant equations:
Set the magnetic force equal to the centripetal force, since the magnetic force is directed towards the center of the particle's circular path and centripetal force is defined as the net force towards the center of a circular path.
Rearrange to isolate the velocity:
Determine the distance, 

Plug this distance and velocity into 

Example Question #1 : Magnetism

Consider a current-carrying loop with current 


A particle with charge 

The correct answer is zero. To calculate the force of a magnetic field on a moving charged particle, we use the cross product. We know that if the magnetic field is parallel to the velocity vector of the particle, then the force produced is zero.
Because our magnetic field in this case is going in the same direction as the velocity of the particle, we know that the magnetic force on the particle is zero.
Example Question #191 : Ap Physics C
Consider two long, straight, current-carrying wires at distance 

If the two wires described are not held in place, what motion will result from the magnetic fields produced?
The wires will move away from each other
The wires will remain in place
The wires will rotate clockwise
The wires will rotate counterclockwise
The wires will move toward each other
The wires will move away from each other
The answer is that the wires will move from each other. Using our right hand rule, we know that the magnetic fields produced by each wire are in the same direction, as long as their currents oppose. Using the right hand rule again to determine the direction of the force exerted on each wire by the magnetic field with which they are interacting yields a force in the direction away from the other wire for each wire.
Certified Tutor
All AP Physics C: Mechanics Resources







![= \frac{b}{4\pi\epsilon_0}\left [ \sqrt{x^2+a^2}\right ]_{0}^{L}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891578/gif.latex)









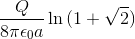






![=\frac{Q}{4\pi\epsilon_{0}a}\left[ \ln\left (\sqrt{x^2+\frac{a^2}{4}} +x\right )\right]_{-a/2}^{a/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891564/gif.latex)