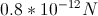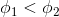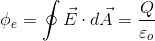All AP Physics C: Mechanics Resources
Example Questions
Example Question #1 : Using Coulomb's Law
Two capacitors are in parallel, with capacitance values of 

The equivalent capacitance for capacitors in parallel is the sum of the individual capacitance values.
Using the values given in the question, we can find the equivalent capacitance.
Example Question #12 : Electricity And Magnetism Exam
A proton moves in a straight line for a distance of 

The charge of a proton is 
The force of an electric field is given by the equation 


Example Question #13 : Electricity And Magnetism Exam
Two point charges, 



The values of the charges are:
The distance is 4.0cm. The point 

What is the magnitude and direction of the net electric field at point 
At point 


At point P, the electric field due to Q2 points away from Q2 with a magnitude given by
The addition of these two vectors, both pointing in the same direction, results in a net electric field vector of magnitude 152000 volts per meter, pointing toward 
Example Question #1 : Using Gauss's Law
A charge, 



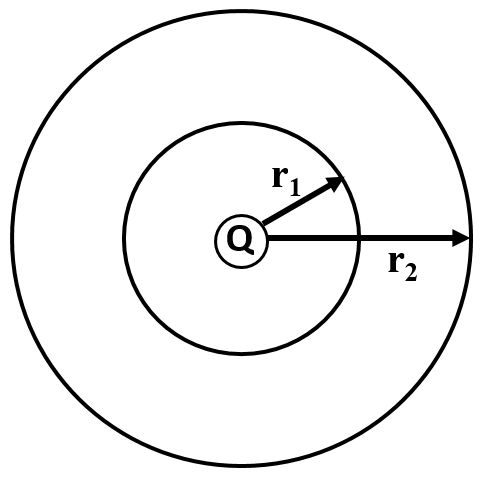
Which is the correct relationship between the electric flux passing through the two spherical surfaces around the point charge?
Electric flux is given by either side of the equation of Gauss's Law:
Since the charge is the same for both spherical surfaces, even though these surfaces are of different radii, the amounts of electric flux passing through each surface is the same.
Example Question #1 : Calculating Electric Potential
A proton moves in a straight line for a distance of 

The charge of a proton is 
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
Example Question #1 : Calculating Electric Potential
For a ring of charge with radius 


Find the expression for electric field produced by the ring.
We know that 
Using the given formula, we can find the electric potential expression for the ring.
Take the derivative and simplify.
Example Question #2 : Calculating Electric Potential
The potential outside of a charged conducting cylinder with radius 

What is the electric field at a point located at a distance 
The radial electric field outside the cylinder can be found using the equation 
Using the formula given in the question, we can expand this equation.
Now, we can take the derivative and simplify.
Example Question #1 : Calculating Electric Potential
A proton moves in a straight line for a distance of 

The charge of a proton is 
Work done by an electric field is given by the product of the charge of the particle, the electric field strength, and the distance travelled.
We are given the charge (


Example Question #1 : Calculating Electric Potential
A negative charge of magnitude 


Relevant equations:
Given:
First, find the potential difference between the initial and final positions:
2. Plug this potential difference into the work equation to solve for W:
Example Question #2 : Calculating Electric Potential
Three point charges are arranged around the origin, as shown.

Calculate the total electric potential at the origin due to the three point charges.
Electric potential is a scalar quantity given by the equation:
To find the total potential at the origin due to the three charges, add the potentials of each charge.
Certified Tutor
All AP Physics C: Mechanics Resources