All AP Physics C Electricity Resources
Example Questions
Example Question #31 : Electricity

A thin bar of length L lies in the xy plane and carries linear charge density 



Use the linear charge density 



Example Question #31 : Electricity

A uniformly charged ring of radius 


Use the linear charge density 





Example Question #11 : Calculating Electric Potential

A uniformly charged square frame of side length 

You may wish to use the integral:
Calculate the potential due to one side of the bar, and then multiply this by 


Example Question #182 : Ap Physics C
Consider a spherical shell with radius 

Zero
Zero
According to the shell theorem, the total electric field at the center point of a charged spherical shell is always zero. At this point, any electric field lines will result in symmetry, canceling each other out and creating a net field of zero at that point.
Example Question #1 : Interpreting Electric Charge Diagrams
A charge of unknown value is held in place far from other charges. Its electric field lines and some lines of electric equipotential (V1 and V2) are shown in the diagram.

A second point charge, known to be negative, is placed at point A in the diagram. In which direction will the second, negative charge freely move?
Toward point A
Toward point C
Toward the original charge Q
It will remain stationary
Toward point C
The original charge Q is negative, as indicated by the direction of the electric field lines in the diagram. A negative point charge of any value placed at point A will cause both charges to feel a mutually repelling force on each other. Therefore, the second charge will be repelled by the original negative charge with a force pointing radially along a line connecting the center of Q and the point A, resulting in free movement toward C. Additionally, point B is on a line of equipotential to point A; negative point charges will move from regions of lower electric potential to higher electric potential (against the direction of the electric field lines), so point B is not a viable answer.
Certified Tutor
All AP Physics C Electricity Resources







![= \frac{b}{4\pi\epsilon_0}\left [ \sqrt{x^2+a^2}\right ]_{0}^{L}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891578/gif.latex)









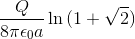






![=\frac{Q}{4\pi\epsilon_{0}a}\left[ \ln\left (\sqrt{x^2+\frac{a^2}{4}} +x\right )\right]_{-a/2}^{a/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891564/gif.latex)









