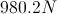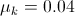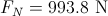AP Physics B : Newtonian Mechanics
Study concepts, example questions & explanations for AP Physics B
All AP Physics B Resources
Example Questions
Example Question #1 : Force Of Friction
A 
The maximum force that can be applied will be equal to the maximum value of the static friction force. The formula for friction is:
We also know that the normal force is equal and opposite the force of gravity.
Substituting to the original equation, we can rewrite the force of friction.
Using the given values for the coefficient of friction and mass, we can calculate the force using the acceleration of gravity.
Example Question #1 : Force Of Friction
A man pulls a 
We must know the mass of the box to solve
Work is equal to the change in energy of the system. We are given the weight of the box and the vertical displacement, which will allow us to calculate the change in potential energy. This will be the total work required to move the box against gravity.
The remaining work that the man exerts must have been used to counter the force of friction acting against his motion.
Now we know the work performed by friction. Using this value, we can work to solve for the force of friction and the coefficient of friction. First, we will need to use a second formula for work:
In this case, the distance will be the distance traveled along the surface of the incline. We can solve for this distance using trigonometry.
We know the work done by friction and the distance traveled along the incline, allowing us to solve for the force of friction.
Finally, use the formula for frictional force to solve for the coefficient of friction. Keep in mind that the force on the box due to gravity will be equal to 
Plug in our final values and solve for the coefficient of friction.
Example Question #1 : Force Of Friction
A 
In order for the crate to not slide, the truck has to exert a frictional force on it. The force of friction is related to the normal force by the coefficient of friction.
This frictional force comes from the acceleration of the truck, based on Newton's second law.
The two forces will be equal when the truck is at maximum acceleration without the crate moving.
Solve for the acceleration.
Example Question #1 : Understanding Friction
A 2kg box is at the top of a ramp at an angle of 60o. The top of the ramp is 30m above the ground. The box is sitting still while at the top of the ramp, and is then released.
Imagine that the net force on the box is 16.5N when sliding down the ramp. What is the coefficient of kinetic friction for the box?
The kinetic coefficient of friction cannot be determined while the box is moving
Since the box is moving when the net force on the box is determined, we can calculate the coefficient of kinetic friction for the box. The first step is determining what the net force on the box would be in the absence of friction. The net force on the box is given by the equation 
The difference between the frictionless net force and the net force with friction is 0.8N. This means that the force of kinetic friction on the box is 0.8N, acting opposite the direction of motion. Knowing this, we can solve for the coefficient of kinetic friction using the equation
Example Question #11 : Forces
A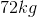 
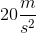
This question essentially asks how much the astronaut will weigh during acceleration. The two forces acting on the astronaut are the downward gravitational force and the upward normal force. The net force acting on this astronaut is 
Notice that the net force is set to equal to 
Isolate the normal force.
Use the given values to solve.
Example Question #13 : Ap Physics 1
A potted plant is hanging from a rope attached to a hook. The plant exerts 25N of force. Assume the rope is weightless.
If the packaging says the rope is able to withstand 800N of force, what is the maximum amount of mass that can be hanging from the rope?
If the rope can only withstand 800N of force, we can solve for the mass of the object which would result in this maximum force when hanging from the rope.
Example Question #1 : Understanding Newton's Laws
A skydiver with a mass of 100kg jumps out of an airplane and reaches a terminal velocity of 
Which of the following factors will not decrease the total force on the man as he jumps from the plane?
The man jumps as the plane is descending sharply
The man immediately opens his parachute
Increasing the man's mass
The man orients his stomach toward the ground, rather than his feet
Increasing the man's mass
The equation for force is 
All other options will result in a decreased acceleration when falling. Falling with his stomach downward increases the surface area of the diver, which increases his air resistance. A parachute will also increase the air resistance and surface area. If the plane is descending when he jumps, his time to reach terminal velocity will be reduced, as he will already have an initial velocity in the downward direction.
Example Question #43 : Forces
A skydiver with a mass of 100kg jumps out of an airplane and reaches a terminal velocity of 
What is the total force acting on the skydiver at this point in his jump?
The man has reached a terminal velocity, which means that he has an acceleration of 
Example Question #1 : Understanding Newton's Laws
A man pushes a crate across a frictionless floor at a constant velocity. Which of the following statements is true?
The force the man exerts on the crate is equal and in the same direction as the force the crate exerts on the man
The force the man exerts on the crate is equal and opposite to the force the crate exerts on the man
The force on the crate is less than the force on the man
The net force on the man is greater than zero
The force on the crate is greater than the force on the man
The force the man exerts on the crate is equal and opposite to the force the crate exerts on the man
According to Newton's third law, the force on the crate must have the same magnitude as the force on the man. The forces must also be in opposite directions. We can conclude that the net force on the man is zero, since he is moving with the crate at a constant velocity.
Example Question #1 : Newton's Second Law
A 2000kg car with a velocity of 
The truck experiences the greater force and the greater acceleration
The car and the truck experience equal force and the car experiences greater acceleration
The car experiences the greater force and the greater acceleration
The truck experiences the greater force and the car experiences the greater acceleration
Both the car and the truck experience equal force and acceleration
The car and the truck experience equal force and the car experiences greater acceleration
The car and the truck experience equal and opposite forces, but since the car has a smaller mass it will experience greater acceleration than the truck according to the equation F = ma.
A greater mass will decrease the acceleration.
All AP Physics B Resources
