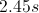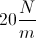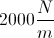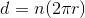We can start this problem by determining how much time it takes the box the reach the ground. Since the vertical distance is 30m and we know the angle of the ramp.

\(\displaystyle \frac{1}{2}=\frac{30m}{x}\rightarrow x=60m\)

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity, using the equation \(\displaystyle \small gsin\Theta\).

\(\displaystyle gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}\)

We can plug these values into the following distance equation and solve for time.

\(\displaystyle \small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}\)

\(\displaystyle \small 0 = 60 - \frac{1}{2}(8.66)t^{2}\)

\(\displaystyle \small \small t = 3.72 s\)

Now that we know the acceleration on the box and the time of travel, we can use the equation \(\displaystyle \small v = v_{0} + at\) to solve for the velocity.

\(\displaystyle \small v = 0 + (8.66\frac{m}{s^{2}})(3.72 s) = 32.2 \frac{m}{s}\)

This is a two step problem. The first step is to calculate the time it takes for the ball to reach the ground. To find this time, we use the following kinematic equation dealing with vertical motion.

\(\displaystyle y=y_o+v_{oy}t+\frac{1}{2}a_yt^2\)

Choosing the ground to be the zero height, we have \(\displaystyle y=0\) and \(\displaystyle y_o=1.2\ \text{m}\).

Also, knowing that the initial vertical velocity is zero, we know that \(\displaystyle v_{oy}=0\).

The kinematic equation simplifies using these values.

\(\displaystyle 0=y_o+\frac{1}{2}at^2\)

Rearrange the equation to isolate time.

\(\displaystyle t=\sqrt{\frac{-2y_o}{a_y}}\)

We know that \(\displaystyle a_y\) is the acceleration due to gravity: \(\displaystyle a_y=-9.8\frac{m}{s^2}\). Plug in the values to solve for time.

\(\displaystyle t=\sqrt{\frac{-2(1.2\ \text{m})}{-9.8\ \frac{\text{m}}{\text{s}^2}}\)

\(\displaystyle t=0.49\ \text{s}\)

We now have the time the ball is travelling before it hits the ground. Use this value to find the horizontal distance before it hits the ground with the kinematic equation \(\displaystyle x=x_0+v_xt\).

We know that \(\displaystyle v_x=9\ \frac{\text{m}}{\text{s}}\) and that \(\displaystyle x_o=0\). Using these values and the time, we can solve for the horizontal distance travelled.

\(\displaystyle x=0+(9\ \frac{\text{m}}{\text{s}})(0.49\ \text{s})\)

\(\displaystyle x=4.4\ \text{m}\)

First, determine how far the car travels in each direction:

\(\displaystyle d=v*t\)

\(\displaystyle (25\frac{m}{s})*(60s)=1500m\ N\)

\(\displaystyle (30\frac{m}{s})*(120s)=3600m\ E\)

Now that we have the directional displacements, we can find the total displacement by using the Pythagorean Theorem.

\(\displaystyle \sqrt{1500^2+3600^2}=3900m\)

Find the average velocity by dividing the total displacement by the total time.

\(\displaystyle v=\frac{\Delta x}{\Delta t}\)

\(\displaystyle v= \frac{3900m}{60s+120s} =21.7\frac{m}{s}\)

Velocity is a vector, meaning it has both magnitude and direction. Now that we have the magnitude, we can find the direction by using trigonometry.

\(\displaystyle \tan\theta=\frac{opp}{adj}=\frac{\Delta x_N}{\Delta x_E}\)

Use the north and the east directional displacements to find the angle.

\(\displaystyle \tan\theta=\frac{1500m}{3600m}\)

\(\displaystyle \theta=\tan^{-1}(\frac{1500m}{3600m})=22.6^o\)

Our final answer will be:

\(\displaystyle 21.7\frac{m}{s}\ \text{at}\ 22.6^o\ \text{above the horizontal}\)

Any projectile has a vertical velocity of zero at the peak of its flight. To solve this question, we need to find the time that it takes the ball to reach this height. The easiest way is to solve for the initial vertical velocity using trigonometry, and then use the appropriate kinematics equation to determine the time.

\(\displaystyle v_f = v_i + at\)

We know that the final vertical velocity will be zero. We can solve for the initial vertical velocity using the given angle and total velocity.

\(\displaystyle v_{iy}=v_o\sin(\theta)\)

\(\displaystyle v_{iy}=(8\frac{m}{s})\sin(30^o)=4\frac{m}{s}\)

Using this in our kinematics formula, we solve for the time.

\(\displaystyle v_f = v_i + at\)

\(\displaystyle 0\frac{m}{s} = (4\frac{m}{s}) + (-9.8\frac{m}{s^2})(t)\)

\(\displaystyle t=\frac{-4\frac{m}{s}}{-9.8\frac{m}{s^2}}\)

\(\displaystyle t=0.41s\)

Keep in mind that this is only the vertical velocity. The total velocity at the peak is not zero, since the ball will still have horizontal velocity.

We can start this problem by determining how far the box will travel on the ramp before hitting the ground. Since the vertical distance is 30m and we know the angle of the ramp, we can determine the length of the hypotenuse using the equation \(\displaystyle \small cos(60^{\circ}) = \frac{30}{x}\).

\(\displaystyle \frac{1}{2}=\frac{30m}{x}\rightarrow x=60m\)

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity. Because the box is on a sloped surface, the box will not experience the full acceleration of gravity, but will instead be accelerated at a value of \(\displaystyle \small gsin\Theta\). Since the angle is 60^o, the acceleration on the box is \(\displaystyle \small 8.66 \frac{m}{s^{2}}.\) 

\(\displaystyle gsin\Theta=(10)sin(60)=8.66\frac{m}{s^2}\)

Finally, we can plug these values into the following distance equation and solve for time.

\(\displaystyle \small x = x_{0} - \frac{1}{2}(gsin\Theta )t^{2}\)

\(\displaystyle \small 0 = 60 - \frac{1}{2}(8.66)t^{2}\)

\(\displaystyle \small \small t = 3.72 s\)

We use Hooke's law equation to relate the force, displacement, and spring constant:

\(\displaystyle F_s=-kx\)

We are given the force and the displacement, allowing us to solve for the spring constant.

\(\displaystyle 100N=-k(-0.05m)\)

Note that the displacement is negative, since the spring is compressed. For springs, compressions represents a negative displacement, while stretching represents a positive displacement.

\(\displaystyle k=\frac{100N}{0.05m}=2000\frac{N}{m}\)

First, we need to solve for the spring constant by using the force on the spring. We can use Hooke's Law:

\(\displaystyle F=-kx\)

The magnitude of the force on the spring will be equal to the force of gravity on the mass, which is given to be \(\displaystyle 20N\). The distance the spring it stretched is in the downward direction, so we must use a negative displacement. Use these values to calculate the spring constant.

\(\displaystyle F=(20N)=-k(-0.10m)\)

\(\displaystyle k=200\frac{N}{m}\)

Next, use the spring energy equation with the displacement and spring constant to solve for the energy stored in the spring.

\(\displaystyle E=\frac{1}{2}kx^2\)

\(\displaystyle E=\frac{1}{2}(200\frac{N}{m})(-0.10m)^2\)

\(\displaystyle E=1J\)

First, we calculate the kinetic energy of the block as it slides:

\(\displaystyle KE=\frac{1}{2}mv^2\)

\(\displaystyle KE=\frac{1}{2}(4kg)(2.5\frac{m}{s})^2=12.5J\)

We know that all of the kinetic energy is converted to spring potential energy during the collision. We can use the equation for the potential energy of a spring and set it equal to the kinetic energy. Then, solve for the compression distance:

\(\displaystyle KE=U_{spring}=\frac{1}{2}kx^2\)

\(\displaystyle 12.5J=\frac{1}{2}(30\frac{N}{m})(x)^2\)

\(\displaystyle x^2=\frac{12.5J}{\frac{1}{2}(30\frac{N}{m})}=0.833m^2\)

\(\displaystyle x=\sqrt{0.833m^2}=0.91m\)

In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is \(\displaystyle 2\pi r\). This means that in one rotation, the wheel would travel a distance equal to its circumference.

Distance of one rotation equals: 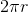\(\displaystyle 2\pi r\).

Since the wheel travels \(\displaystyle n\) rotations, the total distance that the wheel travels will be equal to the distance traveled by one rotation multiplied by the number of rotations.

Distance of \(\displaystyle n\) rotations equals: \(\displaystyle n(2\pi r)\)

\(\displaystyle d=n(2\pi r)\)

We use the equation for centripetal force to find the radius:

\(\displaystyle F_c=\frac{mv^2}{r}\)

Since the string ties the ball to the axis, the force of tension will be equal to the centripetal force.

\(\displaystyle F_T=15N=\frac{mv^2}{r}\)

Use the given mass and velocity to solve for the radius.

\(\displaystyle 15N=\frac{(1kg)(3\frac{m}{s})^2}{r}\)

\(\displaystyle r=\frac{9\frac{m^2kg}{s^2}}{15N}=0.6m\)