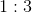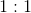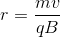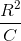All AP Physics B Resources
Example Questions
Example Question #1 : Electricity And Magnetism
Charges A and B are placed a distance of 




A student places these two charges in a vacuum medium and measures 

The dielectric constant of glass is 
You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).
The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.
Example Question #1 : Understanding Electrostatics
How much work is done by the electric field moving an electron along an equipotential surface with a potential of 
We must know the strength of the electric field to solve
Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.
If the potential difference is zero then the energy (and work) will be zero.
Example Question #1 : Ap Physics 2
Charges A and B are placed a distance of 




What is the ratio of 

This question is very simple if you realize that the force experienced by both charges is equal.
The definition of the two electrostatic forces are given by Coulomb's law:
In this question, we can rewrite this equation in terms of our given system.
It doesn’t matter if the charges of the two particles are different; both particles experience the same force because the charges of both particles are accounted for in the electrostatic force equation (Coulomb's law). This conclusion can also be made by considering Newton's third law: the force of the first particle on the second will be equal and opposite the force of the second particle on the first.
Since the forces are equal, their ratio will be 
Example Question #1231 : Ap Physics 1
An excess charge of 



Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:
1) The excess charge on an ideal conducting sphere is uniformly distributed over its surface
2) A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center
With these realizations, an application of Coulomb’s law answers the question. If 

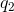
In this equation, 



Using the given values in this equation, we can calculate the generated force:
Example Question #2 : Magnetic Force
A proton traveling at 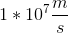


The proton’s mass is 


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
Example Question #1 : Electricity And Magnetism
An ideal transformer, under a purely resistive load, consists of an iron core that directs all the magnetic flux from a primary winding through a secondary winding. The primary winding has 


In basic consideration, the electrical transformer works directly according to Faraday’s law, following the picture given below.

If the coils are wound tightly enough that the magnetic flux generated in any of them effectively passes undiminished through all of them, and the iron core directs all the magnetic flux from the primary to secondary coil with insignificant losses, then Faraday’s law points a direct path from 

If there are 

From the figure, it is seen that the voltages in each line are dropped over all loops together. Hence, for the primary winding, by Faraday’s law:
For the secondary winding:
Here, 


This can be used to solve the problem above:
NOTE: This only works under alternating current. Otherwise, there is no change in current to create the changing magnetic flux on which the transformer depends.
Example Question #1 : Understanding Capacitors
Which of the following is equal to the time constant of an RC circuit?
The definition of a time constant for an RC circuit is the product of resistance and charge:
This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
Example Question #3 : Ap Physics 2
Which of the following statements is false regarding capacitors?
I. A larger capacitor stores more energy
II. Capacitors connected in parallel have the same voltage drop
III. Increasing the distance between the two plates increases the capacitance
II and III
III only
I and III
I only
I and III
Recall the equation for potential energy in terms of capacitance:
According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.
Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.
Remember that capacitance is defined as follows:
In this equation, 


Example Question #1 : Electricity And Magnetism
A capacitor has a stored charge of 

To solve this problem, you need to use the following two equations:
By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.
Rearranging the previous equation will allow us to solve for the voltage.
Use the given values for stored potential energy and charge to solve for the voltage.
Example Question #1 : Electricity And Magnetism
A 





Our first step will be to find the equivalent resistance of the circuit. Simple resistors add in series, and add inversely in parallel. For the 

For the resistors in parallel, the inverse of the total resistance is equal to the sum of the inverse of the individual resistors.
The total resistance of the circuit will be the sum of the series resistance and parallel resistance.
Now we know the total resistance of the circuit and the voltage supplied from the battery. Use Ohm's law to solve for the current in the circuit.
Certified Tutor
Certified Tutor
All AP Physics B Resources