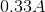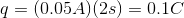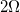
Recall that the current through resistors connected in series is the equal for all components. The current through the first resistor and the current through the second resistor should be the same.

The first step in solving involves calculating the equivalent resistance of the circuit. Since the resistors are in series the equivalent resistance of this circuit is the sum of the two resistances.

Now we can use Ohm’s law to solve for the current.

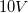
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:

The definition of electric current is given by the charge per unit time:

Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.

Now that we know the current and the time, we can solve for the charge using our second equation.

The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.

Remember that power is defined as work per unit time:

The units from this equation will be Joules per second, eliminating that answer choice.

In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:

If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:

These units will be Amperes squared times Ohms.

The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:

Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.

Remember the equations for voltage and power. The equation for voltage is Ohm's law:

Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:

From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.

According to Ohm’s law a decrease in current and/or resistance will lead to a decrease in voltage, since voltage is directly proportional to both current and resistance.

Increasing the current will not decrease voltage. Remember that resistance is defined as:

In this formula, is the resistivity, is the length of the wire, and  is the cross-sectional area of the wire. Increasing length will lead to an increase in resistance and voltage; however, increasing the area will lead to a decrease in resistance and, subsequently, a decrease in voltage.

The only answer that will lead to a decrease in voltage is the choice to increase the cross-sectional area of the wire.

Replacing the copper wire with a more conductive material will increase the resistivity, which will subsequently increase resistance and voltage.

When circuit elements, such as resistors, are connected in parallel they will have the same voltage drop. The current through the resistor will be greater than current through the resistor, but their voltages will be equal. According to Ohm’s law the current flowing through the smaller resistor will be larger. Ohm’s law can be rearranged to solve for current as follows:

Since voltage is the same across resistors, the lower resistance () will have more current flowing through it since current is inversely proportional to resistance.