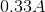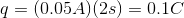Recall the equation for potential energy in terms of capacitance:

According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.

Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.

Remember that capacitance is defined as follows:

In this equation, is the area of the plates and  is distance between the plates. Increasing  will lead to a decrease in capacitance; therefore, statement III is false.

To solve this problem, you need to use the following two equations:

By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.

Rearranging the previous equation will allow us to solve for the voltage.

Use the given values for stored potential energy and charge to solve for the voltage.

Our first step will be to find the equivalent resistance of the circuit. Simple resistors add in series, and add inversely in parallel. For the  and  resistors in series, the total resistance is simply the sum.

For the resistors in parallel, the inverse of the total resistance is equal to the sum of the inverse of the individual resistors.

The total resistance of the circuit will be the sum of the series resistance and parallel resistance.

Now we know the total resistance of the circuit and the voltage supplied from the battery. Use Ohm's law to solve for the current in the circuit.

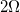
Recall that the current through resistors connected in series is the equal for all components. The current through the first resistor and the current through the second resistor should be the same.

The first step in solving involves calculating the equivalent resistance of the circuit. Since the resistors are in series the equivalent resistance of this circuit is the sum of the two resistances.

Now we can use Ohm’s law to solve for the current.

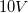
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:

The definition of electric current is given by the charge per unit time:

Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.

Now that we know the current and the time, we can solve for the charge using our second equation.

The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.

Remember that power is defined as work per unit time:

The units from this equation will be Joules per second, eliminating that answer choice.

In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:

If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:

These units will be Amperes squared times Ohms.

The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:

Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.

Remember the equations for voltage and power. The equation for voltage is Ohm's law:

Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:

From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.

The relationship between frequency and energy is determined by Planck's constant in a direct relationship. This means that as frequency increases, energy increases as well.

The electromagnetic waves with the highest frequency will have the greatest energy per photon, and vice versa.

In the electromagnetic spectrum, radio waves have the lowest frequency (largest wavelength) and gamma rays have the highest frequency (shortest wavelength). Gamma rays will thus have the highest frequency and greatest energy.

The amplitudes of in-phase waves add in what is called constructive interference. We can find the resultant amplitude of the first two waves by adding their individual amplitudes.

The third wave is out of phase, meaning that it will contribute destructive interference when the three waves align. We subtract the amplitude of the third wave from the total of the first two.

This is the final amplitude of the resultant wave.

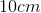
For the thin lens equation, the convention for image distance is positive on the opposite side of the lens from the object. In effectively all practical cases for a single thin lens, positive image distance corresponds to a real image, and negative to a virtual. Convex lenses effectively only produce real images for objects outside their focal distance. Based on these initial observations, certain answer choices can be eliminated.

Use the thin lens equation to choose between the remaining answer options.

In the equation,  is the object distance, or ;  is the focal length, or ; and  is the image distance from the lens.

Since the object distance is twice the focal length, the image distance will be as well.  So , and the image is real, which can be confirmed with a quick ray diagram

.

The ray diagram for a simple thin lens can be constructed according to three rules that apply, in their own way, either to converging or diverging lenses (convex or concave):

1. A ray traveling parallel to the optical axis gets bent by the lens so as to pass, or appear to pass, through the focal point.

2. A ray traveling through the center of the lens is not deviated.

3. A ray passing through, or appearing to pass through, the focal point of the lens is bent parallel to the optical axis.

Following these rules, it can be seen that the convex lens brings the light rays to a real focus at the image position, and the image would fall on a screen placed at that point to create a real image.

Note:  This configuration represents what is called “ to ” imaging, where the object is twice as far from the convex lens as its focal length, and thus the image is as well. It turns out that, for a simple convex lens, this is the smallest total object-to-image distance attainable for a real image.