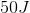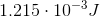In parallel branches of a circuit, the voltage drops are all the same. Therefore, we know that the voltage drop across C3 is also 5V.

We can then use the following equation to calculate the total stored energy:

Since the voltage is the same for both capacitors, we can simply add the two capacitances to do one calculation for energy:

To find the amount of energy stored in a capactior, we use the equation

.

We're given the capacitance (), and the voltage (), so we'll use the third equation.

The equation for energy stored in a capacitor is 

We can find the capacitance by adding the capacitors together, and we have the voltage, so we'll use the second equation, .

When adding capacitors, remember how to add in series and parallel.

Capacitors  and  are in series,  and  are in parallel, and  and  are in parallel.

Now that we have the total capacitance, we can use the earlier equation to find the energy.

The total energy stored is 121.5J. 

In this circuit, the voltage source,  and , and  are all in parallel, meaning they share the same voltage.

To find the energy, we can use the formula

, with  being the energy,  being the capacitance, and being the voltage drop across that capacitor.

To use the formula we need the voltage across .

Another hint we can use is that  and  having the same charge since they're in series. First let's find the equivalent capacitance:

Now, we can use the formula 

 to calculate charge in the capacitor.

Now that we know a charge of  exists in both capacitors, we can use the formula again to find the voltage in only .

Finally, we plug this  into the first equation to calculate energy.

Equations required:

We see from the first equation the when D is doubled, C will be halved (since  and  are constant). From the third equation, we seed that when C is halved, the potential energy, U will double.

Relevant equations:

We must note for this problem that the voltage, V, is kept constant by the battery. Looking at the second equation, if C changes (by changing D) then Q must change when V is held constant. This means that our formula for U must be altered. How can we make claims about U if Q and C are both changing? We need a constant variable in the equation for U so that we can make a direct relationship between D and U. If we plug in the second equation into the third we arrive at:

Now, we know that V is held constant by the battery, so when C decreases (because D doubled) we see that U actually decreases here. So it matters whether or not the capacitor is hooked up to a battery.

The reason dielectrics reduce the effective electric field strength is because when a dielectric is added, the medium gets polarized, which produces an electric field in opposition of the existing electric field. 

When the electric field decreases, the capacitance increases because the plates are able to store more charge for the same amount of voltage applied, because there's less force repelling electrons from gathering on the plate.

The equation for capacitance of parallel conducting plates is:

When the distance is doubled, the capacitance changes to:

The battery is still connected to the plates, the potential difference is unchanged. Because , and the capacitance is halved while the voltage stays the same,  must necessarily drop to half to account for the change.

Recall the equations used for adding capacitors:

From the diagram, capacitors A and B are in parallel, and capacitors C and D are in parallel, and those two systems are in series.

Use the equation above to find the equivalent capacitance of capacitors A and B.

Use the equation above to find the equivalent capacitance of capacitors C and D. 

Use the equation above to find the total capacitance by adding the two systems of capacitors, which are in series.

Therefore, the total capacitance is

The equations for adding capacitors are:

To find the total energy, we need to know the total capacitance. To do that, we the capacitors together according to the rules above.

Capacitors A and B are in parallel.

Capacitors C and D are in parallel.

Add the systems of capacitors together. They are in series. 

The total capacitance is

The equation for finding the energy of a capacitor is:

Plug in known values and solve.

Therefore, the system, when fully charged, holds  of energy.