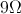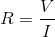We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics 2 : AP Physics 2

Study concepts, example questions & explanations for AP Physics 2

Create An Account

All AP Physics 2 Resources

6 Diagnostic Tests 149 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : Circuits

What is the resistance in a wire carrying a voltage of 10V and with a power of ?

Possible Answers:

$16\Omega$

$6.25\Omega$

$25\Omega$

$2.5\Omega$

$1.6\Omega$

Correct answer:

$25\Omega$

Explanation:

The formula we can use here is the power formula that involved both resistance and voltage:

$P=\frac{V^2}{R}$

We are given the voltage and power, allowing us to solve for the resistance.

$4W=\frac{(10V)^2}{R}$

$R=\frac{100V^2}{4W}$

$R=25\Omega$

Report an Error

Example Question #61 : Ap Physics 2

A $\small 12V$ battery supplies power to a circuit with a current of $\small 16A$ . What is the resistance in this circuit?

Possible Answers:

$12\Omega$

$0.75\Omega$

$9\Omega$

$192\Omega$

$1.33\Omega$

Correct answer:

$0.75\Omega$

Explanation:

To find resistance from voltage and current, we will need to use Ohm's law:

V=IR

$R= \frac{V}{I}$

We are given the voltage and current, allowing us to solve for the resistance.

$R = \frac{12V}{16A} = 0.75\Omega$

Report an Error

Example Question #2 : Resistivity

An electrician wishes to cut a copper wire $(\rho = 1.724 * 10^{-8}\Omega m)$ that has no more than $10 \Omega$ of resistance. The wire has a radius of 0.725mm. Approximately what length of wire has a resistance equal to the maximum $10 \Omega$ ?

Possible Answers:

2.6cm

960m

38m

9.6m

10cm

Correct answer:

960m

Explanation:

To relate resistance R, resistivity $\rho$ , area A, and length L we use the equation $R = \frac{\rho L}{A}$ .

Rearranging to isolate the quantity we wish to solve for, L, gives the equation $L = \frac{RA}{\rho }$ . We must first solve for A using the radius, 0.725mm.

$A = \pi r^{2} = \pi (0.000725m)^{2}=1.65 * 10^{-6}m^{2}$

Plugging in our numbers gives the answer, 960m.

$L = \frac{10\Omega * 1.65 * 10^{-6}m^{2}}{1.724*10^{-8}\Omega m} = 957m \approx960m$

Report an Error

Example Question #1 : Resistors And Resistance

During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.

Screen_shot_2013-10-09_at_11.08.15_pm

What is the net resistance of the circuit?

Possible Answers:

$4\Omega$

$9\Omega$

$2\Omega$

$2.5\Omega$

$11\Omega$

Correct answer:

$4\Omega$

Explanation:

First we need to combine the resistors in parallel.

$\frac{1}{R_{A4}}=\frac{1}{R_A}+\frac{1}{R_4}$

$\frac{1}{R_{A4}}=\frac{1}{6\Omega }+\frac{1}{3\Omega}=\frac{1}{2}\Omega$

By taking the inverse of the equation, we can see that R_A4 is equal to 2Ω.

Now that we have simplified the two resistors in parallel, we need to determine how the R_eq of the two parallel resistors and the resistance due to R₁ are arranged. We can see that these resistors are now in series, thus we can directly add their resistances together to get the overall resistance of the circuit.

R_eq = R_A4 + R₁ = 2Ω + 2Ω = 4Ω

Remember as a general rule, the equivalent resistance of resistors in series is an arithmetic sum of their individual resistances.

Report an Error

Example Question #2 : Voltage, Energy, And Power

Screen_shot_2013-10-09_at_11.08.15_pm

Instead of assuming that the 9V battery has no internal resistance, what would the terminal potential of the battery be if it has an internal resistance of $0.9\Omega$ ?

Possible Answers:

6.975V

2.394V

8.1V

4.643V

Correct answer:

6.975V

Explanation:

Remember that internal resistance lowers the EMF of the battery. We need to calculate the voltage drop that would occur inside the battery, and then subtract that from the “stated” voltage to determine the terminal potential of the battery.

We first need the current supplied by the battery. We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.

$\frac{1}{R_{A4}}=\frac{1}{R_A}+\frac{1}{R_4}$

$\frac{1}{R_{A4}}=\frac{1}{6\Omega }+\frac{1}{3\Omega}=\frac{1}{2}\Omega$

By taking the inverse of the equation, we can see that R_A4 is equal to 2Ω.

R_eq = R_A4 + R₁ = 2Ω + 2Ω = 4Ω

Now, using V=IR, we can find the current in the circuit.

V = IR

I = V/R = 9V/4Ω = 2.25A

Plugging in this value with the internal resistance of the battery gives us the voltage decrease.

V = IR = (2.25A)(0.9Ω) = 2.025V

Terminal Potential = 9V – 2.025V = 6.975V

As we can see, battery companies are interested in keeping the internal resistance of batteries at a minimum, because it lowers the overall terminal potential of the battery.

Report an Error

Example Question #1 : Capacitors And Dielectrics

Capacitors with capacitances of 3 μF, 7 μF and 10 μF are wired in parallel. What is the capacitance of the circuit?

it cannot be determined without knowing the resistance of the circuit
it cannot be determined without knowing the time constant in the circuit
20 μF
approximately 1.75 μF
none of these is correct

Possible Answers:

Correct answer:

Explanation:

Response 3 is the correct choice. Electrons will space themselves as far apart as possible, because of charge repulsion; therefore, in a parallel arrangement, they will jump onto each capacitor and “load it up.” The parallel capacitance is calculated by simply adding the individual values. The value would be about 1.75 μF if the three were connected in series, where the formula is $\dpi{100} \small \frac{1}{C_{total}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}$ (reciprocal of total equals sum of reciprocal of each). The time constant of a circuit is given by the formula τ = RC, and it relates to how fast a capacitor can charge to full capacitance.

Report an Error

Example Question #1 : Capacitors And Dielectrics

A $2\mu F$ and $6\mu F$ capacitor are connected in series with a 12V battery. What is the maximum charge stored on the $2\mu F$ capacitor?

Possible Answers:

$4.5 \mu C$

$18\mu C$

$13.5 \mu C$

$96 \mu C$

$24 \mu C$

Correct answer:

$18\mu C$

Explanation:

First find the equivalent capacitance of the two capacitors by adding their inverses.

$\frac{1}{C_{eq}}=\frac{1}{2}+\frac{1}{6}$ $\rightarrow C_{eq} = \frac{6}{4} = 1.5\mu F$

Then, we can find the charge stored on this equivalent capacitor.

$Q_{eq}=C_{eq}V = 1.5 * 12 = 18\mu C$

For capacitors in series the charges on each must be equal, and also equal to the charge on the equivalent capacitor. The answer is $18\mu C$ .

Report an Error

Example Question #2 : Capacitors And Dielectrics

Batteries and AC current are often used to charge a capacitor. A common example of capacitor use is in computer hard drives, where capacitors are charged in a specific pattern to code information. A simplified circuit with capacitors can be seen below. The capacitance of C₁ is 0.5 μF and the capacitances of C₂ and C₃ are 1 μF each. A 10 V battery with an internal resistance of 1 Ω supplies the circuit.

Pretext Question_2

How is the charge stored on the capacitor?

Possible Answers:

Evenly distributed inside the capacitor

Evenly distributed on the capacitor surface

Unevenly distributed on the capacitor surface

Unevenly distributed inside the capacitor

Correct answer:

Evenly distributed on the capacitor surface

Explanation:

Charge is evenly distributed on the surface of the capacitor. If we think back to electric force, we know that positive charges repel other positive charges and negative charges repel other negative charges; thus, the charges are evenly distributed to minimize the force between them. We can see how this looks in diagrammatic form below.

Charge_dist

Report an Error

Example Question #1 : Capacitors And Dielectrics

Pretext Question_2

What is the equivalent capacitance of C₂ and C₃?

Possible Answers:

0.33μF

0.5μF

3μF

2μF

Correct answer:

0.5μF

Explanation:

First, we need to determine how these capacitors are being added. We can see that they are being added in in series. Remember that capacitors in series are added as reciprocals:

$\frac{1}{C_{eq}}=\frac{1}{C_2}+\frac{1}{C_3}=\frac{1}{1\mu F}+\frac{1}{1\mu F}=2\mu F$

C_eq = 0.5μF

Report an Error

Example Question #71 : Electricity And Magnetism

Pretext Question_2

What is the equivalent capacitance of the circuit?

Possible Answers:

4μF

3μF

1μF

2μF

Correct answer:

1μF

Explanation:

First, we need to determine how capacitors C₂ and C₃ are being added. We can see that they are being added in in series. Remember that capacitors in series are added as reciprocals.

$\frac{1}{C_{23}}=\frac{1}{C_2}+\frac{1}{C_3}=\frac{1}{1\mu F}+\frac{1}{1\mu F}=2\mu F$

C₂₃ = 0.5μF

Next, we need to determine how we can find the C_eq by simplifying C₂₃ and C₁. We can see that C_eq and C₁are in parallel, thus we can directly add the individual capacitances.

C_eq = C₂₃ + C₁ = 0.5μF + 0.5μF = 1μF

Report an Error

View Tutors

Adair
Certified Tutor

Marymount College, Bachelor of Science, Chemistry.

View Tutors

Paarth
Certified Tutor

New Jersey Institute of Technology, Bachelor of Science, Computer Science.

View Tutors

Joshua
Certified Tutor

Murray State University, Bachelor in Arts, Spanish. Lipscomb University, Bachelor of Science, Teacher Assistant.

All AP Physics 2 Resources

6 Diagnostic Tests 149 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Phoenix, Biology Tutors in San Diego, Math Tutors in Dallas Fort Worth, Biology Tutors in Washington DC, French Tutors in Houston, Statistics Tutors in Phoenix, Calculus Tutors in Phoenix, GRE Tutors in New York City, French Tutors in Denver, SSAT Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Seattle, GRE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in San Diego, ISEE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Denver, SAT Courses & Classes in Boston, SAT Courses & Classes in Seattle, MCAT Courses & Classes in Houston, ISEE Courses & Classes in Seattle

Popular Test Prep

LSAT Test Prep in New York City, ISEE Test Prep in Philadelphia, LSAT Test Prep in Denver, MCAT Test Prep in Seattle, ACT Test Prep in San Diego, GMAT Test Prep in Washington DC, SAT Test Prep in Seattle, LSAT Test Prep in Seattle, GRE Test Prep in San Diego, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics 2 : AP Physics 2

Study concepts, example questions & explanations for AP Physics 2

All AP Physics 2 Resources

Example Questions

Example Question #5 : Circuits

Example Question #61 : Ap Physics 2

Example Question #2 : Resistivity

Example Question #1 : Resistors And Resistance

Example Question #2 : Voltage, Energy, And Power

Example Question #1 : Capacitors And Dielectrics

Example Question #1 : Capacitors And Dielectrics

Example Question #2 : Capacitors And Dielectrics

Example Question #1 : Capacitors And Dielectrics

Example Question #71 : Electricity And Magnetism

All AP Physics 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: