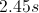The velocity must be broken down into x (horizontal) and y (vertical) components. We can use the y component to find how high the object gets. To find vertical velocity, v_y, use .

Next we find how long it takes to reach the top of its trajectory using .

 t = 5.3s

Finally, find how high the object goes with .

First, find the horizontal (x) and vertical (y) components of the velocity

Next, find how long the object is in the air by calculating the time it takes it to reach the top of its path, and doubling that number.

t = 6.25s 

Total time in the air is therefore 12.5s (twice this value).

Finally, find distance traveled my multiplying horizontal velocity and time.

We can start this problem by determining how much time it takes the box the reach the ground. Since the vertical distance is 30m and we know the angle of the ramp.

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity, using the equation .

We can plug these values into the following distance equation and solve for time.

Now that we know the acceleration on the box and the time of travel, we can use the equation  to solve for the velocity.

This is a two step problem. The first step is to calculate the time it takes for the ball to reach the ground. To find this time, we use the following kinematic equation dealing with vertical motion.

Choosing the ground to be the zero height, we have and .

Also, knowing that the initial vertical velocity is zero, we know that .

The kinematic equation simplifies using these values.

Rearrange the equation to isolate time.

We know that  is the acceleration due to gravity: . Plug in the values to solve for time.

We now have the time the ball is travelling before it hits the ground. Use this value to find the horizontal distance before it hits the ground with the kinematic equation .

We know that  and that . Using these values and the time, we can solve for the horizontal distance travelled.

First, determine how far the car travels in each direction:

Now that we have the directional displacements, we can find the total displacement by using the Pythagorean Theorem.

Find the average velocity by dividing the total displacement by the total time.

Velocity is a vector, meaning it has both magnitude and direction. Now that we have the magnitude, we can find the direction by using trigonometry.

Use the north and the east directional displacements to find the angle.

Our final answer will be:

Any projectile has a vertical velocity of zero at the peak of its flight. To solve this question, we need to find the time that it takes the ball to reach this height. The easiest way is to solve for the initial vertical velocity using trigonometry, and then use the appropriate kinematics equation to determine the time.

We know that the final vertical velocity will be zero. We can solve for the initial vertical velocity using the given angle and total velocity.

Using this in our kinematics formula, we solve for the time.

Keep in mind that this is only the vertical velocity. The total velocity at the peak is not zero, since the ball will still have horizontal velocity.

We can start this problem by determining how far the box will travel on the ramp before hitting the ground. Since the vertical distance is 30m and we know the angle of the ramp, we can determine the length of the hypotenuse using the equation .

Now that we have the distance traveled, we can determine the acceleration on the box due to gravity. Because the box is on a sloped surface, the box will not experience the full acceleration of gravity, but will instead be accelerated at a value of . Since the angle is 60^o, the acceleration on the box is  

Finally, we can plug these values into the following distance equation and solve for time.

First we need to find out at what the speed relative to the ground the plane needs to fly. The plane needs to cover 100 miles in 1 hour, so it's simply 100 mph due north.

Now we need to calculate its speed relative to the wind and its angle. We know the sum of the wind vector and plane vector needs to equal 100 mph due north. Therefore, all east/west movement must cancel out and all north/south movement must add to 100mph.

We can separate the wind velocity into its components:

We can also represent the components of the plane's velocity:

If the trig functions seem reversed, this is because the angle in question is between the y-coordinate and a vector pointing slightly west of north.

We can also represent the components of the velocity relative to the ground:

Since the horizontal velocity is equal to 0, we can set the x-components of the wind and plane vectors equal to each other:

The sum of the y-components of the wind and plane vectors must equal 100:

The wind vector is subtracted because it is in the opposite direction of the plane vector.

Now we just need to isolate a variable and substitute one equation into another. We will isolate the total plane velocity in the first equation:

Substituting this into the second equation, we get:

Solving for theta, we get  (west of north)

We can plug this into the first equation to get:

To solve this problem, we first need to split the velocity into its vector components.

Initial vertical velocity:

Initial horizontal velocity:

Since we are neglecting air resistance, horizontal velocity does not change over time. We only need to calculate the new vertical velocity after two seconds, using kinematics:

The negative sign simply means that the vertical velocity has changed direction, and is now pointed downward.

We can use the following equation to determine the total velocity, which will be the sum of the horizontal and vertical velocity vectors:

We're told that the golf ball is starting its parabolic journey with a certain velocity at an angle to the ground. To solve for the time the golf ball stays airborne, we'll need to consider the x and y-components of the ball's trajectory.

First, we'll need an expression that considers the ball's velocity in the x-direction.

We'll also need an expression for the y-component of the velocity.

We'll need an expression that can relate the vertical distance traveled with the time spent in the air. Since the only acceleration occurring in this scenario is due to gravity, the result is that acceleration is constant. Therefore, we can make use of some of the kinematics equations:

It's also important to note that once the ball lands back on the ground, only its horizontal displacement will have changed, while its vertical displacement will remain unchanged.

We also have to remember that in this case, the source of acceleration is from gravity, which points downwards. If we define up as the positive y direction, then down must be the negative y direction. Therefore, we can write:

Plug in the vertical component of velocity and solve for time.