All AP Physics 1 Resources
Example Questions
Example Question #1 : Tension
Consider the following system:
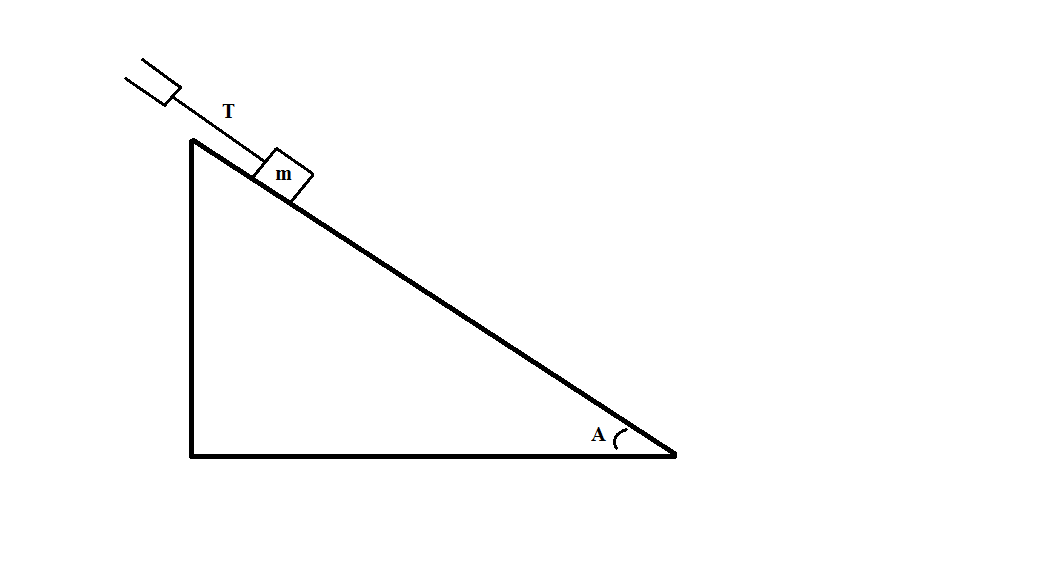
If the mass is 


Since there is no friction between the mass and slope, there are only two relevant forces acting on the mass: gravity and tension. Furthermore, since the block is not in motion, we know that these forces are equal to each other. Therefore:
Substituting in an expression for the force of gravity, we get:
We know all of these values, allowing us to solve for the tension:
Example Question #792 : Ap Physics 1
Consider the following system:

If the force of tension is 



There are three relevant forces acting on the block in this scenario: friction, tension, and gravity. We are given two of these values, so we simply need to develop an expression for the force of gravity in the direction of the slope. Since the block is motionless, we can write:
Substituting in an expression for the force of gravity, we get:
Rearrange to solve for the angle:
We know all of these values, allowing us to solve:
Example Question #1 : Tension
Consider the following system:

If the coefficient of static friction is 


There are three relevant forces acting on the block in this scenario: tension, friction, and gravity. We are given tension, so we will need to develop expressions for friction and gravity. Since the block is motionless, we can say:
Plugging in expressions for the force of gravity and friction, we get:
Rearranging for the mass, we get:
We know all of these values, allowing us to solve:
Example Question #793 : Ap Physics 1
Consider the following system:

If the block has a mass of 


Since there is no tension, there are only two relevant forces acting on the block: friction and gravity. Since the block is motionless, we can also write:
Substitute the expressions for these two forces:
Canceling out mass and gravitational acceleration, and rearranging for the coefficient of static friction, we get:
Example Question #1 : Tension
Consider the following system:

If the mass is accelerating at a rate of 




There are three relevant forces acting on the block in this situtation: friction, gravity, and tension. We can use Newton's second law to express the system:
Substituting expressions in for the forces, we get:
Canceling out mass and rearranging to solve for tension, we get:
We have values for each variable, allowing us to solve:
Example Question #1 : Tension

A 12kg block is sliding down a 

In order to find the mass of block 2, we're going to need to calculate a few other things, such as the tension in the rope.
To begin with, we'll need to identify the various forces on our free-body diagram. To do this, we will begin with block 1 and use a rotated coordinate system to simplify things. In such a system, the x-axis will run parallel to the surface of the ramp, while the y-axis will be perpendicular to the ramp's surface, as shown below:


Now we can identify the forces acting on block 1. Along the rotated y-axis, the force of gravity acting on the block is equal to 

Now, considering the forces acting along the rotated x-axis, we have a force pointing downwards equal to 


The formula for calculating the force due to kinetic friction is:
Since we have already determined what the normal force is, we can substitute that expression into the above equation to obtain:
Now, we can write an expression for the net force acting upon block 1 in the x direction:
Rearrange the above expression to solve for tension.
So far, we have only been looking at block 1. Now let's turn our attention to block 2 and see what forces are acting on it. In the downward direction we have the weight of the block due to gravity, which is equal to 

Since we calculated the expression for tension from the information regarding block 1, we can plug that expression into the above equation in order to obtain:
Now rearrange to solve for the mass of block 2.
Then plugging in values, we can finally calculate block 2's mass:
Example Question #191 : Forces
What is the tension force on a wire holding a 10kg ball 20ft above the ground, if the ball is not moving at that height?
Since the gravitational force must be cancelled by the tension force, as the ball is experiencing no acceleration, and no other forces are being applied to it:
Example Question #1 : Tension
A block weighing 

The block has three forces on it: the force of tension, the force of gravity, and the force from Bruce. The force of gravity is:
The force from Bruce plus the force of tension has to equal gravity (since Bruce's force and tension are up while gravity is down) so the block is in equilibrium.
Example Question #10 : Tension
A helicopter is lifting a box of mass 

Plug in values:
Solve for
Example Question #761 : Newtonian Mechanics
Earth mass:
Earth's distance from the Sun:
Velocity of the Earth:
Imagine that, instead of gravity, the earth was attached to the sun with a giant, unbreakable rope. Determine what the tension would be in the rope.
The velocity of the earth is
Convert to 
Plug in values:
Certified Tutor
Certified Tutor
All AP Physics 1 Resources







































































![m_{2}a=[m_{1}gsin(\theta )-\mu _{k}m_{1}gcos(\theta )-m_{1}a]-m_{2}g](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/454498/gif.latex)

![m_{2}=\frac{[m_{1}gsin(\theta )-\mu _{k}m_{1}gcos(\theta )-m_{1}a]}{(a+g)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/454500/gif.latex)
![m_{2}=\frac{[(12kg*9.8\frac{m}{s^{2}}* sin(30^{o}))-(0.18* 12kg* 9.8\frac{m}{s^{2}}* cos(30^{o}))-(12kg* 1.5\: \frac{m}{s^{2}})]}{(1.5 \frac{m}{s^{2}}+9.8 \frac{m}{s^{2}})}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/454501/gif.latex)














































