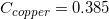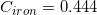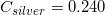We need to find the specific heat of the unknown sample of metal in order to locate it on the list. We can do this by using the equation that allows us to determine the specific heat capacity of an element.

$\displaystyle \small q = mC\Delta T$

Since we know the change in temperature, we can simply plug in the values and solve for the value of $\displaystyle \small C$.

$\displaystyle \small 800J = (50g)C(41.6^oC)$

$\displaystyle \small C = 0.385$

Going back to the list, we see that this is the specific heat capacity for copper, so we confirm that the unknown metal is copper. 

Bomb calorimeters are most useful when dealing with a gas, because they can operate well at high pressures. Coffee-cup calorimeters are not useful when water begins to boil, producing vapor.

You need heat for the phase change, using the enthalpy of fusion (100g*334 J/g = 33400 J). Add to this the heat to get to boiling point using the specific heat of water (100g*100C*4.2 J/g^oC = 42000 J). Totalling 75400 J (75.4 kJ)

First we will determine the mass of the liquid:

$\displaystyle 300\hspace{1 mm}mL\times\frac{0.0321\hspace{1 mm}g}{1\hspace{1 mm}mL}=9.63\hspace{1 mm}g$

Now we will examine the relationship between heat and specific heat capacity:

$\displaystyle Q=cm\Delta T$

Where $\displaystyle Q$ is heat in Joules, $\displaystyle c$ is the specific heat capacity, $\displaystyle m$ is the mass and $\displaystyle \Delta T$ is the change in temperature. We can rearrange this

$\displaystyle \Delta T=\frac{Q}{cm}$

$\displaystyle \Delta T=\frac{243\hspace{1 mm}J}{0.32J\cdot kg^{-1}\cdot K^{-1}0.00963kg}=78855\hspace{1 mm}K$

If we begin at $\displaystyle 27.1^{\circ}C$, we will end at $\displaystyle 78882^{\circ}C$

When the heated metal is placed in the container of the cooler water there will be a transfer of thermal energy from the metal to the water.  This transfer will occur towards an equilibrium of thermal energy in the water and in the metal. Thus we can conclude that the amount of thermal energy lost by the metal will equal the amount of thermal energy gained by the water.  However we notice that the water increases by only 5^oC  and the metal decreases by 65^oC.  This is becasue of the difference of the specific heats of these substances.  The specific heat capacity of a substance is the heat required to increase the temperature of 1g of a substance by 1^oC. The metal can be conluded to have a smaller specific heat than the water because the same amount of energy transfer led to a much larger change in termperature for the metal as compared to the water.  

4.184 J/gK is the cited value for the specific heat of water and should be memorized. This is used during calorimeter calculations, specifically when using the equation q= mc delta(T).

This question involves the total energy needed for three different processes: the temperature raise from $\displaystyle \small -10^oC$ to $\displaystyle \small 0^oC$, the melting of the ice, and the temperature raise from $\displaystyle \small 0^oC$ to $\displaystyle \small 35^oC$. For the first and third transitions we will use the equation $\displaystyle \small q=mC\Delta T$. For the melting of ice, we will use the equation $\displaystyle q=m\Delta H_{fusion}$.

1. $\displaystyle \small \small q =m_{ice}C_{ice}\Delta T = (5g)(0.5\frac{cal}{g^{\circ}C})(10^{\circ}C) = 25 cal$

2. $\displaystyle \small q = m\Delta H_{fusion} = (5g)(80\frac{cal}{g}) = 400 cal$

3. $\displaystyle \small q = m_{water}C_{water}\Delta T = (5g)(1.0\frac{cal}{g^{\circ}C})(35^{\circ}C) = 175 cal$

Finally, we will need to sum the energy required for each step to find the total energy.

$\displaystyle 25cal+400cal+175cal=600cal$

$\displaystyle Q=m\cdot C\cdot\Delta T$

Since the density of water is $\displaystyle 1.00\, \frac{g}{mL}$, the mass of $\displaystyle 100\,mL$ is $\displaystyle 100\,g$. Plug in known values to the equation and solve.

$\displaystyle 100g\cdot\frac{4.184J}{g^{\text o}C}\cdot \left ( 60 - 20 \right )^{\text o}C=16736J$

Use the formula below to find the time needed to heat up the sample of water in the microwave:

$\displaystyle P=\frac{\Delta W}{\Delta t}$

$\displaystyle \Delta t=\frac{16736J}{700W}=23.9s$

Our answer must contain three significant figures.

To find the amount of heat needed to change the temperature of a given material by a certain amount, we'll need to use the equation for specific heat. The specific heat capacity of a compound represents the amount of energy necessary to raise $\displaystyle 1$ gram of that substance by $\displaystyle 1\: ^{o}C$.

$\displaystyle q=mC\Delta T$

$\displaystyle q=(5\: grams)(0.900\: \frac{J}{g\cdot ^{o}C})(20\: ^{o}C)=90\:J$

There are two things to note before solving for the final temperature.

1. The density of water allows us to say that 300 milliliters of water is the same thing as 300 grams of water.

$\displaystyle 300mL*\frac{1g}{1mL}=300g$

2. Since the heat from the iron is being transferred to the water, we can say that the heat transfer is equal between both compounds. Since the heat is conserved in the system, we can set the two equations equal to one another.

$\displaystyle q=mC\Delta T$

$\displaystyle q_i=q_w\rightarrow m_iC_i\Delta T=m_wC_w\Delta T$

$\displaystyle \small m_{i}C_{i}(T_{initial}-T_{final}) = m_{w}C_{w}(T_{final}-T_{initial})$

Notice how the change in temperature for iron has been flipped in order to avoid a negative number.

$\displaystyle \small (20g)(0.444\frac{J}{g^{\circ}C})(120^{\circ}C-T_{f}) = (300g)(4.184\frac{J}{g^{\circ}C})(T_{f}-30^{\circ}C)$

$\displaystyle \small T_{f} = 30.63^{\circ}C$

Because water has a much higher heat capacity compared to iron, the temperature of the water is not changed significantly.