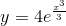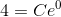We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus BC : Integrals

Study concepts, example questions & explanations for AP Calculus BC

Create An Account

All AP Calculus BC Resources

2 Diagnostic Tests 86 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Give the arclength of the graph of the function $f(x) = \frac{2}{3} x \sqrt{x}$ on the interval $\left [ 0,3 \right ]$ .

Possible Answers:

$\frac{14}{3}$

$\frac{11}{3}$

$\frac{16}{3}$

Correct answer:

$\frac{14}{3}$

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f(x) = \frac{2}{3} x \sqrt{x} = \frac{2}{3} x^{\frac{3}{2}}$

$f(x) = \frac{2}{3} \cdot \frac{3}{2} x^{\frac{1}{2}} = \sqrt{x}$ .

The above integral becomes

$\int_{0}^{3} \sqrt{1 + (\sqrt{x}) ^{2}} \; \mathrm{d}x$

$\int_{0}^{3} \sqrt{x+1} \; \mathrm{d}x$

Substitute u = x + 1 . Then $\frac{\mathrm{d} u}{\mathrm{d} x} = 1$ , $\mathrm{d} u = \mathrm{d} x$ , and the integral becomes

$\int_{1}^{4} \sqrt{u} \; \mathrm{d}u = \int_{1}^{4} u^{\frac{1}{2}} \; \mathrm{d}u$

$= \left.\begin{matrix} \frac{u^{\frac{3}{2}}}{\frac{3}{2}} \\ \\ \end{matrix}\right| \begin{matrix} 4\\ \\ 1 \end{matrix}$

$= \left.\begin{matrix} \frac{2u \sqrt{u}}{3} \\ \\ \end{matrix}\right| \begin{matrix} 4\\ \\ 1 \end{matrix}$

$= \frac{2 \cdot 4 \sqrt{4}}{3} - \frac{2 \cdot 1 \sqrt{1}}{3}$

$= \frac{2 \cdot 4 \cdot 2 }{3} - \frac{2 \cdot 1 \cdot 1}{3} = \frac{16}{3} - \frac{2}{3} =\frac{14}{3}$

Report an Error

Example Question #12 : Application Of Integrals

Give the arclength of the graph of the function $f(x) = \frac{1}{2} \ln \left ( \cos 2 x \right )$ on the interval $\left [ 0, \frac{\pi}{8} \right ]$ .

Possible Answers:

$\ln \left ( 1 + \sqrt{2} \right )$

$1+\frac{1 }{2} \ln 2$

$\frac{1 }{2}+\frac{1 }{2} \sqrt{2}$

$\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right )$

$1 + \sqrt{2}$

Correct answer:

$\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right )$

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f(x) = \frac{1}{2} \ln \left ( \cos 2 x \right )$ , so

$f'(x) = \frac{1}{2} \cdot \frac{\frac{\mathrm{d} }{\mathrm{d} x}\cos 2 x}{\cos 2 x} = \frac{1}{2} \cdot \frac{-2 \sin 2x}{\cos 2 x} = - \tan 2x$

The integral becomes

$\int_{0}^{ \frac{\pi}{8}} \sqrt{1 + \left ( - \tan 2x \right )^{2}} \; \mathrm{d}x$

$= \int_{0}^{ \frac{\pi}{8}} \sqrt{1 + \tan ^{2} 2x } \; \mathrm{d}x$

$= \int_{0}^{ \frac{\pi}{8}} \sqrt{\sec ^{2} 2x } \; \mathrm{d}x$

$= \int_{0}^{ \frac{\pi}{8}} \sec 2x \; \mathrm{d}x$

Use substitution - set u = 2x . Then $\frac{\mathrm{d} u}{\mathrm{d} x} = 2$ , and $\mathrm{d} x = \frac{1}{2}\mathrm{d} u$ . The bounds of integration become $2 \cdot 0 = 0$ and $2 \cdot \frac{\pi}{8} = \frac{\pi}{4}$ , and the integral becomes

$\frac{1}{2} \int_{0}^{ \frac{\pi}{4}} \sec u \; \mathrm{d}u$

$=\left.\begin{matrix}\frac{1}{2} \ln | \sec u + \tan u | \\ \\ \end{matrix}\right|\begin{matrix} \frac{\pi}{4}\\ \\ 0 \end{matrix}$

$=\frac{1}{2} \ln \left | \sec \frac{\pi}{4} + \tan \frac{\pi}{4} \right | - \frac{1}{2} \ln | \sec 0 + \tan 0 |$

$=\frac{1}{2} \ln \left | \sqrt{2} + 1 \right | -\frac{1}{2} \ln | 1 + 0 |$

$=\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right ) -\frac{1}{2} \ln 1$

$=\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right ) - 0$

$=\frac{1}{2} \ln \left (1 + \sqrt{2} \right )$

Report an Error

Example Question #1 : Average Values And Lengths Of Functions

What is the length of the curve $g(x)=x^{\frac{3}{2}}$ over the interval $0\le x\le4$ ?

Possible Answers:

$\frac{4\pi}{3}$

$\frac{56}{27}$

$\frac{8}{27}(10\sqrt{10}-1)$

$4\sqrt2-1$

Correct answer:

$\frac{8}{27}(10\sqrt{10}-1)$

Explanation:

The general formula for finding the length of a curve f(x) over an interval [a,b] is $\int_{a}^{b}\sqrt{1+\left(\frac{dy}{dx}\right)^2}\ dx$

In this example, the arc length can be found by computing the integral

$\int_{0}^{4}\sqrt{1+(\frac{d}{dx}x^{\frac{3}{2}})^2}\ dx$ .

The derivative of $x^{\frac{3}{2}}$ can be found using the power rule, $\frac{d}{dx} x^n=nx^{n-1}$ , which leads to

$\int_{0}^{4}\sqrt{1+\left(\frac{3}{2}x^{\frac{1}{2}}\right)^2}\ dx=\int_{0}^{4}\sqrt{1+\frac{9}{4}x}\ dx$ .

At this point, a substitution is useful.

Let

$u=1+\frac{9}{4}x,\ du=\frac{9}{4}dx,\frac{4}{9}du=dx$ .

We can also express the limits of integration in terms of to simplify computation. When x=0, u=1 , and when x = 4, u=10 .

Making these substitutions leads to

$\int_{0}^{4}\sqrt{1+\frac{9}{4}x}\ dx=\int_{1}^{10}\frac{4}{9}\sqrt{u}du=\frac{4}{9}\int_{1}^{10}u^{\frac{1}{2}}du$ .

Now use the power rule, which in general is $\int x^n=\frac{x^{n+1}}{n+1}+c$ , to evaluate the integral.

$\frac{4}{9}\int_{1}^{10}u^{\frac{1}{2}}du=\frac{4}{9}\frac{u^{\frac{3}{2}}}{\frac{3}{2}}|_{1}^{10}$

$=\frac{8}{27}(10^{\frac{3}{2}}-1^\frac{3}{2})=\frac{8}{27}(10\sqrt{10}-1)$

Report an Error

Example Question #1 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Find the total distance traveled by a particle along the curve y=x^2 from x=0 to x=2 .

Possible Answers:

$\int_0^2\sqrt{1+4x^2}dx$

$\int_0^2\sqrt{1+2x}dx$

$\int_0^2\sqrt{1+2x^2}dx$

$\int_0^2\sqrt{1+x^2}dx$

$\int_0^2\sqrt{1+4x^2}dx$

Correct answer:

$\int_0^2\sqrt{1+4x^2}dx$

Explanation:

To find the required distance, we can use the arc length expression given by $\int_{x_0}^{x_1}\sqrt{1+f'(x)^2}dx$ .

Taking the derivative of our function, we have y'=f'(x)=2x . Plugging in our values for our integral bounds, we have

$\int_0^2\sqrt{1+(2x)^2}dx = \int_0^2 \sqrt{1+4x^2}dx$ .

As with most arc length integrals, this integral is too difficult (if not, outright impossible) to evaluate explicitly by hand. So we will just leave it this form, or evaluate it with some computer software.

Report an Error

Example Question #1 : Modeling By Solving Separable Differential Equations

Solve the separable differential equation

$\frac{\mathrm{d} y}{\mathrm{d} x}= yx^2$

with the condition y(0)=4 .

Possible Answers:

$y=Ce^{\frac{x^3}{3}}$

$y=4e^{\frac{x^3}{3}}$

$y=Ce^{\frac{x^2}{2}}$

$y=4e^{\frac{x^2}{3}}$

$y=Ce^{\frac{64}{3}}$

Correct answer:

$y=4e^{\frac{x^3}{3}}$

Explanation:

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

$\frac{dy}{y}=x^2dx$

Integrating both sides, we get

$\ln\left | y\right |=\frac{ x^3}{3}+C$

The rules of integration used were

$\int \frac{dx}{x}=\ln\left | x\right |+C$ , $\int x^ndx= \frac{x^{n+1}}{n+1}+C$

The constants of integration merged into one.

Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

$y=e^{\frac{x^3}{3}}+e^C=e^{{\frac{x^3}{3}}\cdot C}=Ce^{\frac{x^3}{3}}$

To solve for C, we use our given condition:

4=Ce^0

4=C

Our final answer is

$y=4e^{\frac{x^3}{3}}$

Report an Error

View AP Calculus BC Tutors

James
Certified Tutor

University of Georgia, Bachelor in Arts, Political Science and Government.

View AP Calculus BC Tutors

Leo
Certified Tutor

Columbia International University, Bachelor of Science, Chemistry.

View AP Calculus BC Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

All AP Calculus BC Resources

2 Diagnostic Tests 86 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in San Diego, ACT Tutors in Atlanta, SSAT Tutors in Washington DC, Physics Tutors in Philadelphia, LSAT Tutors in Denver, Statistics Tutors in San Francisco-Bay Area, Statistics Tutors in Boston, SSAT Tutors in Boston, GRE Tutors in Dallas Fort Worth, LSAT Tutors in Seattle

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, LSAT Courses & Classes in Boston, GRE Courses & Classes in Phoenix, SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Seattle, Spanish Courses & Classes in Miami, SSAT Courses & Classes in Chicago, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in New York City, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Chicago, SAT Test Prep in Houston, SAT Test Prep in Phoenix, GRE Test Prep in Seattle, SAT Test Prep in Chicago, SSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Dallas Fort Worth, LSAT Test Prep in San Diego, SSAT Test Prep in Philadelphia, SAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus BC : Integrals

Study concepts, example questions & explanations for AP Calculus BC

All AP Calculus BC Resources

Example Questions

Example Question #2 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Example Question #12 : Application Of Integrals

Example Question #1 : Average Values And Lengths Of Functions

Example Question #1 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Example Question #1 : Modeling By Solving Separable Differential Equations

All AP Calculus BC Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: