All AP Calculus BC Resources
Example Questions
Example Question #2 : Improper Integrals
Evaluate 
By the Formula Rule, we know that 

Continuing the calculation:
By the Power Rule for Integrals, 



So,
![=\lim_{b\rightarrow \infty }[-{\frac{1}{b^{4}}+1}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382524/gif.latex)

Example Question #1 : Substitution Of Variables (By Parts And Simple Partial Fractions)
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Example Question #2 : Substitution Of Variables (By Parts And Simple Partial Fractions)
Integrate:
To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
Example Question #1 : Applications In Physics
The temperature of an oven is increasing at a rate 


What is the temperture of the oven at 
Integrating 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/403013/gif.latex)
to find the change in temperature that occurs during the first five minutes.
A substitution is useful in this case. Let




To evaluate this, you must know the antiderivative of an exponential function.
In general,

Therefore,

This tells us that the temperature rose by approximately 


Example Question #2 : Integral Applications
Find the equation for the velocity of a particle if the acceleration of the particle is given by:
and the velocity at time 

In order to find the velocity function, we must integrate the accleration function:
We used the rule

to integrate.
Now, we use the initial condition for the velocity function to solve for C. We were told that
so we plug in zero into the velocity function and solve for C:
C is therefore 30.
Finally, we write out the velocity function, with the integer replacing C:
Example Question #1 : Initial Conditions
Find the work done by gravity exerting an acceleration of 


Remember that







The force of gravity is proportional to the mass of the object and acceleration of the object.
Since the block fell down 5 meters, its final position is 

Example Question #1 : Application Of Integrals
Evaluate the following integral and find the specific function which satisfies the given initial conditions:
Evaluate the following integral and find the specific function which satisfies the given initial conditions:
To solve this problem,we need to evaluate the given integral, then solve for our constant of integration.
Let's begin by recalling the following integration rules:
Using these two, we can integrate f(x)
SO, we get:
We are almost there, but we need to find c. To do so, plug in our initial conditions and solve:
So, our answer is:
Example Question #1 : Volume Of Cross Sections And Area Of Region
Determine the volume of the solid obtained by rotating the region with the following bounds about the x-axis:
From calculus, we know the volume of an irregular solid can be determined by evaluating the following integral:
Where A(x) is an equation for the cross-sectional area of the solid at any point x. We know our bounds for the integral are x=1 and x=4, as given in the problem, so now all we need is to find the expression A(x) for the area of our solid.
From the given bounds, we know our unrotated region is bounded by the x-axis (y=0) at the bottom, and by the line y=x^2-4x+5 at the top. Because we are rotating about the x-axis, we know that the radius of our solid at any point x is just the distance y=x^2-4x+5. Now that we have a function that describes the radius of the solid at any point x, we can plug the function into the formula for the area of a circle to give us an expression for the cross-sectional area of our solid at any point:
We now have our equation for the cross-sectional area of the solid, which we can integrate from x=1 to x=4 to find its volume:
Example Question #2 : Volume Of Cross Sections And Area Of Region
Suppose the functions 


Write the formula for cylindrical shells, where 

Determine the shell radius.
Determine the shell height. This is done by subtracting the right curve, 

Find the intersection of 

The bounds will be from 0 to 2. Substitute all the givens into the formula and evaluate the integral.
Example Question #3 : Volume Of Cross Sections And Area Of Region
Find the volume of the solid generated by revolving the region bounded by 


Since we are revolving a region of interest around a horizontal line 
Recall the formula:
The outer radius is 



Using trigonometric identities, we know that:
Hence:
Certified Tutor
Certified Tutor
All AP Calculus BC Resources













![=\lim_{b\rightarrow \infty }4[-{\frac{1}{4b^{4}}-(-\frac{1}{4}})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382522/gif.latex)
![=\lim_{b\rightarrow \infty }4[-{\frac{1}{4b^{4}}+\frac{1}{4}})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382523/gif.latex)


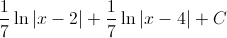


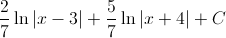


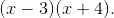






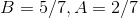
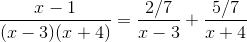
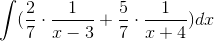






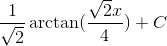



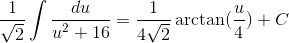




















































![=\pi [\frac{1}{5}x^5-2x^4+\frac{26}{3}x^3-20x^2+25x]_{1}^{4}=\frac{78\pi }{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265347/gif.latex)












![V=2\pi \left[ 2y^2 - \frac{1}{4}y^4\right]_{0}^{2} = 2\pi \left[2(2)^2 -\frac{1}{4}(2)^4\right] = 2\pi[8-4]= 8\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/288906/gif.latex)





![Volume = \pi \int_{b}^{a} [(\textup{outer radius})^{2} - (\textup{inner radius})^{2}]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343034/gif.latex)



![= \pi \left[\frac{1}{2}x - \frac{1}{4}sin2x\right]_{0}^{\pi} = \frac{1}{2}\pi^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343042/gif.latex)



