All AP Calculus AB Resources
Example Questions
Example Question #82 : Numerical Approximations To Definite Integrals
Using the Trapezoidal Rule with four subintervals, approximate to four decimal places:
The Trapezoidal Rule states that a definite integral

can be approximated by computing the expression
where 
Since we are dividing ![\left [ 2,3 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971476/gif.latex)

where
Example Question #41 : Trapezoidal Sums
Solve in the integral by method of trapezoidal sums
To use the trapezoidal rule, we apply the following formula:
Using the integral from our problem statement, we get
Example Question #311 : Integrals
Evaluate the integral using the trapezoidal sums method:
To solve the integral, we will use the formula for the trapezoidal sums method:
Using the integral from the problem statement, we get
Simplifying, we end up with
Example Question #1115 : Ap Calculus Ab
Evaluate using the trapezoidal approximation:
The trapezoidal approximation of a definite integral is given by
For our integral, we get
Example Question #1116 : Ap Calculus Ab
Use the method of trapezoidal sums to approximate the integral
To approximate the integral using trapezoidal sums, we use the following formula:
Using the integral from the problem statement, we get
Example Question #83 : Numerical Approximations To Definite Integrals
Using the method of trapezoidal sums, evaluate the following integral
To find the value of the integral, we use the following formula
Example Question #1117 : Ap Calculus Ab
Using the method of trapezoidal sums, evaluate the following integral
To use the method of trapezoidal sums, we follow the definition
Using the information from the problem statement, we get
Example Question #1121 : Ap Calculus Ab
Use the trapezoidal approximation to solve the definite integral, and find the difference between it and the actual integral:
The trapezoidal approximation to definite integrals is given by
Using this formula for our integral, we get
Actually integrating, we get
The rule used for integration is
The difference between the approximation and the actual answer is
Example Question #1122 : Ap Calculus Ab
Approximate the value of 

6
4
2
10
5
4
Trapezoidal sums are found by creating trapezoids whose left and right end points are on the specified function, and whose widths are the step size. We then sum up their areas by remembering that the area of a trapezoid is the base times the average of the heights.
Thus, the calculation of the trapezoidal sum for this example would be
A more simplified version would be given by
Which evaluates to
The actual answer is found by evaluating the definite integral given, which would just be given by
The difference between the approximation and the the true answer is thus
Certified Tutor
All AP Calculus AB Resources







![T_{N}=\frac{b-a}{2N} \left [f (x_{0} ) +2 f (x_{1}) +2 f ( x_{2} ) + ... 2f ( x_{N-1} )+ f (x_{N} ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/962657/gif.latex)

![T_{4}=\frac{1}{8} \left [ f(2 ) +2 f \left (2.25 \right ) +2 f \left (2.5 \right ) + 2f \left ( 2.75 \right ) + f (3 ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971478/gif.latex)






![T_{4}=\frac{1}{8} \left [ 1.2619 +2 (1.4763 )+2 ( 1.6681)+ 2 ( 1.8416) +2 \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971485/gif.latex)






![\int_{a}^{b}f(x)dx\approx(b-a)\left [ \frac{f(a)-f(b)}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971740/gif.latex)



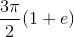


![\int_{a}^{b}f(x)dx=(b-a)\left [ \frac{f(a)+f(b)}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/979090/gif.latex)
![(2\pi-\frac{\pi}{2})\left [ \frac{e^{\sin(2\pi)}+e^{\sin(\frac{\pi}{2})}}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/979091/gif.latex)













![\int_{a}^{b} f(x)dx=(b-a)\left [ \frac{f(b)+f(a)}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/988169/gif.latex)
![(1-0)\left [ \frac{(\frac{4-e}{5})+(\frac{-1}{5})}{2} \right ]=\frac{3-e}{10}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/988170/gif.latex)





+f(b)}{2})](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1001222/gif.latex)
e^\frac{\pi}{2}+\sin(0)e^0}{2})=\frac{\pi}{4}e^\frac{\pi}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1001223/gif.latex)





![\int_{a}^{b}f(x)dx=(b-a)\left [ \frac{f(a)+f(b)}{2}\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1006331/gif.latex)











![2 \cdot [\frac{f(-2)+f(0)}{2}] + 2 \cdot [\frac{f(0)+f(2)}{2}] + 2 \cdot [\frac{f(2)+f(4)}{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1033834/gif.latex)


![\int_{-2}^{4} x^2 dx = \left . \frac{x^3}{3} \right ]^4_{-2} = \frac{4^3 - (-2)^3}{3} = \frac{64 + 8}{3} = \frac{72}{3} = 24](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1033837/gif.latex)




