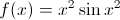All AP Calculus AB Resources
Example Questions
Example Question #19 : Asymptotic And Unbounded Behavior
Compute
The limit does not exist.
Firstly, recall the rules for evaluating the limits of rational expressions as they go to infinity:
If the degree on the top is greater than the degree on the bottom, the limit does not exist.
If the degree on the top is less than the degree on the bottom, the limit is 0.
If the degrees in both the numerator and denominator are equal, the limit is the ratio of the leading coefficients.
These rules follow from how the function grows as the inputs get larger, ignoring everything but the leading terms.
Then, note that, while the numerator is not written in the correct order for you, that the highest power in the numerator is 5. Likewise, the highest power in the denominator is 5. Thus, the limit will be the ratio of the coefficients on the 

Example Question #20 : Asymptotic And Unbounded Behavior
Evaluate
The equation 
We can find the horizontal asymptote by looking at the terms with the highest power.
The terms with the highest power here are 

The ratio is
Example Question #21 : Functions, Graphs, And Limits
Find 
First step for finding limits: evaluate the function at the limit.

This got us nowhere. However, since we have an indeterminate form, we can use L'Hopital's Rule (take the derivative of the top and bottom and the limit's value won't change).
This is something we can evaluate:
The value of this limit is 
Example Question #22 : Functions, Graphs, And Limits
Assume that a population of bunnies grows at a rate of where


Note: No integration is required for this problem.
700
5
70
350

350
The equation given is a model of logistic growth. Note that one of the other common forms this equation might be given in is . What we want to know is what the population will be given unlimited time, or what
is.
Looking at the form of the derivative above, note that if we start with 14 bunnies, we get a positive derivative. This means that the population is increasing. As our function is continuous, the population will keep growing until the derivative hits 0. When does this occur?
In the above form, it should be more clear that the derivative is only 0 at 

Example Question #23 : Functions, Graphs, And Limits
The function 
The function will produce only positive outputs.
The function is discontinuous at y=0.
None of the other answers.
At x=0 the function is undefined.
The limit of the function as x-values approach 0 tends to either positive or negative infinity.
None of the other answers.
Unlike vertical asymptotes, horizontal asymptotes of certain functions may be crossed. In these cases, and in the case of the given function, the horizontal asymptote may be crossed and even have defined values laying on it (e.g., f(0)=0 for the function provided).
What is meaningful about the horizontal asymptote in this example is that it suggests the behavior of the function at large magnitudes. The denominator will increase much faster than the numerator. That is to say that the 

Example Question #24 : Functions, Graphs, And Limits
Is the following piecewise function continuous for all 
No. The function is not continuous at both 

No. The function is not continuous at 
No. There are sharp turns at 

Yes. The function is continuous at all 
No. The function is not continuous at 
Yes. The function is continuous at all 
To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.
At 



Plugging 3 into both, we see that both of them are 12 at 
Next, for 


As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.
Note, there are sharp turns at 

Example Question #21 : Functions, Graphs, And Limits
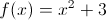


At 
neither differentiable or continuous
undefined
differentiable but not continuous
continuous but not differentiable
both continuous and diffentiable
both continuous and diffentiable
The answer is both.
If graphed the student will see that the two graphs are continuous at 
Example Question #471 : Derivatives
Which of the following functions contains a removeable discontinuity?
A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at 



For example, the function 




Thus, we could say that 
As we can see, the limit of 


What this means is that 




The functions

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.
The functions



The answer is

Example Question #1 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change
Evaluate the definite integral of the algebraic function.
integral (x3 + √(x))dx from 0 to 1
1
11/12
10/12
0
5/12
11/12
Step 1: Rewrite the problem.
integral (x3+x1/2) dx from 0 to 1
Step 2: Integrate
x4/4 + 2x(2/3)/3 from 0 to 1
Step 3: Plug in bounds and solve.
[14/4 + 2(1)(2/3)/3] – [04/4 + 2(0)(2/3)/3] = (1/4) + (2/3) = (3/12) + (8/12) = 11/12
Example Question #1 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change
Evaluate the integral.
Integral from 1 to 2 of (1/x3) dx
–3/8
1/2
–5/8
0
3/8
3/8
Integral from 1 to 2 of (1/x3) dx
Integral from 1 to 2 of (x-3) dx
Integrate the integral.
from 1 to 2 of (x–2/-2)
(2–2/–2) – (1–2/–2) = (–1/8) – (–1/2)=(3/8)
Certified Tutor
Certified Tutor
All AP Calculus AB Resources