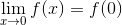You can substitute  to write this as:

Note that as , 

, since the fraction becomes indeterminate, we need to take the derivative of both the top and bottom of the fraction.

, which is the correct choice.

Substitute  to rewrite this limit in terms of u instead of x. Multiply the top and bottom of the fraction by 2 in order to make this substitution:

(Note that as , .)

, so

, which is therefore the correct answer choice.

To evaluate the limit, we must first determine whether the limit is right or left sided; the minus sign exponent indicates we are approaching three from the left, or using values slightly less than three. These correspond to the first part of the piecewise function, whose limit is 9 (substitution). 

To evaluate the limit, we must first determine whether we are approaching 4 from the left or right; the positive sign exponent indicates that this is a right side limit, or that we are approaching using values slightly greater than 4. When we substitute this into the function, we find that we approach , as the natural logarithm function approaches this when its domain goes to zero. 

First, try evaluating the limit at the target value.

This gives us an indeterminate form, so we have to keep trying. Let's factor the polynomials:

We can cancel an , so let's do that.

Now evaluate at the target value.

The limit evaluates to .

Unless we are explicitly told so, via graph, information, or otherwise, we cannot assume  is continuous at  unless , which is required for  to be continuous at .

We cannot assume anything about the existence of , because we do not know what  is, or its end behavior.

The limit of a function as  approaches a value  exists if and only if the limit from the left is equal to the limit from the right; the actual value of  is irrelevant. Since the function is piecewise-defined, we can determine whether these limits are equal by finding the limits of the individual expressions. These are both polynomials, so the limits can be calculated using straightforward substitution:

 does not exist, because .

For a function to be continuous the following criteria must be met:

1.  The function must exist at the point (no division by zero, asymptotic behavior, negative logs, or negative radicals). 
2. The limit must exist.
3. The point must equal the limit. (Symbolically, ).

It is easiest to first find any points where the function is undefined. Since our function involves a fraction and a natural log, we must find all points in the domain such that the natural log is less than or equal to zero, or points where the denominator is equal to zero.

To find the values that cause the natural log to be negative we set 

Therefore, those x values will yield our points of discontinuity. Normally, we would find values where the natural log is negative; however, for all  the function is positive. 

The mid-point Reimann sum is given by this formula:

, where , and  is the number of 

intervals.  Thus, if the region from  to  is divided into twenty intervals,  and .  For ten intervals,  and .  For five internals,  and .  The higher the number of intervals, the more precise the estimation.  Thus, when  (and hence ), the estimation is the most accurate.  

For this value, the Limit Laws can be applied: