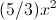We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Functions, Graphs, and Limits

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #33 : Limits Of Functions (Including One Sided Limits)

f(x) Discgraph

True or false: In the above graph of f(x) , the value of $\lim_{x\rightarrow -4}f(x)$ is 3.

Possible Answers:

True: The removable discontinuity does not affect the limit, and the right and left limits evaluate to 3.

False: We can't take the limit where the function isn't defined.

False: The left and right limits exist, but neither of them is three.

False: The left and right limits exist, but exactly one of them isn't three.

False: Both the left and right limits are three, but the regular limit isn't.

Correct answer:

True: The removable discontinuity does not affect the limit, and the right and left limits evaluate to 3.

Explanation:

Removable discontinuities don't affect the limiting process. The limit process is essentially saying "As you get arbitrarily close to x = -4 , the function is getting arbitrarily close to ." As you can see, whether or not the function is defined at is irrelevant, because we're want to look at values close to it, but never exactly at .

Graphically, we can see that the left and right limits are both three. If you trace the graph from either the left or right of , you will end up at .

By definition, if both the right and left limit evaluate to the same thing, the actual limit must agree. It's not possible for both of them to be three, but for the limit to disagree with them (at least in a two dimensional graph!)

Thus the correct answer is that the limit exists, and is three.

Report an Error

Example Question #172 : Functions, Graphs, And Limits

f(x)

Discgraph

In the above graph of f(x) , evaluate the following limits:

$\lim_{x\rightarrow 4^+} f(x)$

$\lim_{x\rightarrow 4^-} f(x)$

$\lim_{x\rightarrow 4} f(x)$

Possible Answers:

$\lim_{x\rightarrow 4^+}f(x) \: \mathrm{Does \: Not \: Exist}$

$\lim_{x\rightarrow 4^-}f(x) =3$

$\lim_{x\rightarrow 4}f(x) \: \mathrm{Does \: Not \: Exist}$

$\lim_{x\rightarrow 4^+}f(x) =5$

$\lim_{x\rightarrow 4^-}f(x) =3$

$\lim_{x\rightarrow 4}f(x) = 3$

$\lim_{x\rightarrow 4^+}f(x) =3$

$\lim_{x\rightarrow 4^-}f(x) =3$

$\lim_{x\rightarrow 4}f(x) = 3$

$\lim_{x\rightarrow 4^+}f(x) =3$

$\lim_{x\rightarrow 4^-}f(x) =5$

$\lim_{x\rightarrow 4}f(x) \: \mathrm{Does \: Not \: Exist}$

$\lim_{x\rightarrow 4^+}f(x) =5$

$\lim_{x\rightarrow 4^-}f(x) =3$

$\lim_{x\rightarrow 4}f(x) \: \mathrm{Does \: Not \: Exist}$

Correct answer:

$\lim_{x\rightarrow 4^+}f(x) =5$

$\lim_{x\rightarrow 4^-}f(x) =3$

$\lim_{x\rightarrow 4}f(x) \: \mathrm{Does \: Not \: Exist}$

Explanation:

A right limit is found graphically by starting at a point to the right of the specified x value and tracing along the graph to the left until you hit the specified x. Regardless of whether or not the function is defined, or perhaps if its defined, but not where your finger ends up, your finger should be at the limit. This is because limits don't concern themselves with what happens at the specified x value. For right limits, we're essentially asking "If I get arbitrarily close to x=4 from the right, what is f(x) getting close to?"

The same holds true for left limits, but you approach them from the other side.

In this problem, $\lim_{x\rightarrow 4^+}f(x)$ is a right limit. Following the above method, we find that as we approach x =4 from the right, we end up at . Similarly, $\lim_{x\rightarrow 4^-}f(x)$ is a left limit. Approaching x =4 from the left, we see that we arrive at .

Lastly, a regular limit is defined when both the right and left limits are defined and equal. In this case, the right limit is 5 and the left limit is 3, so the regular limit does not exist

Report an Error

Example Question #1 : Understanding The Limiting Process.

Find the derivative.

y = sec (5x³)

Possible Answers:

y' = –csc(5x³)cot(5x³)(15x²)

y' = –sec(5x³)tan(5x³)(15x²)

y' = sec(5x³)tan(5x³)(15x²)

y' = –csc(5x³)cot(5x³)

y' = sec(5x³)tan(5x³)

Correct answer:

y' = sec(5x³)tan(5x³)(15x²)

Explanation:

The derivative of the function y = sec(x) is sec(x)tan(x). First take the derivative of the outside of the function: y = sec(4x³) : y' = sec(5x³)tan(5x³). Then take the derivative of the inside of the function: 5x³ becomes 15x². So your final answer is: y' = ec(5x³)tan(5x³)15x²

Report an Error

Example Question #1 : Understanding The Limiting Process.

Find the slope of the tangent line to the graph of f at x = 9, given that f(x) = –x²+ 5√(x)

Possible Answers:

–18 + (5/6)

–18

–18 – (5/6)

18 + (5/6)

Correct answer:

–18 + (5/6)

Explanation:

First find the derivative of the function.

f(x) = –x² + 5√(x)

f'(x) = –2x + 5(1/2)x^–1/2

Simplify the problem

f'(x) = –2x + (5/2x^1/2)

Plug in 9.

f'(3) = –2(9) + (5/2(9)^1/2)

= –18 + 5/(6)

Report an Error

Example Question #2 : Understanding The Limiting Process.

Find the derivative

(x + 1)/(x – 1)

Possible Answers:

(–2)/(x + 1)²

(x + 1) + (x – 1)

(–2)/(x – 1)²

(–2)/(x – 1)

Correct answer:

(–2)/(x – 1)²

Explanation:

Rewrite problem.

(x + 1)/(x – 1)

Use quotient rule to solve this derivative.

((x – 1)(1) – (x + 1)(1))/(x – 1)²

(x – 1) – x – 1)/(x – 1)²

–2/(x – 1)²

Report an Error

Example Question #35 : Limits Of Functions (Including One Sided Limits)

$\frac{d}{dx}sin^{-1} (3x)$

Possible Answers:

$\frac{3x}{\sqrt{1-9 x^2}}$

$\frac{3}{\sqrt{1-9 x^2}}$

$\frac{3x}{\sqrt{1- x^2}}$

$\frac{3}{\sqrt{1-3x^2}}$

Correct answer:

$\frac{3}{\sqrt{1-9 x^2}}$

Explanation:

Use the chain rule and the formula

$\frac{d}{dx}sin^{-1}u = \frac{1}{\sqrt{1-x^2}}$

Report an Error

Example Question #4 : Understanding The Limiting Process.

Find the derivative of

$f(x)=4(x^{3}-2x+11)(x-2)$

Possible Answers:

$4x^{4}-8x^{3}-8x^{2}+60x-22$

24x-2

$f'(x)=16x^{3}-24x^{2}-16x+60$

$4(3x^{2}-2)$

$3x^{2}-8x+15$

Correct answer:

$f'(x)=16x^{3}-24x^{2}-16x+60$

Explanation:

The answer is $f'(x)=16x^{3}-24x^{2}-16x+60$ . It is easy to solve if we multiply everything together first before taking the derivative.

$f(x)=4(x^{3}-2x+11)(x-2)$

$f(x)=4(x^{4}-2x^{3}+-2x^{2}+4x+11x-22)$

$f(x)=4x^{4}-8x^{3}-8x^{2}+60x-22$

$f'(x)=16x^{3}-24x^{2}-16x+60$

Report an Error

Example Question #4 : Calculus 3

Find $\frac{d^{2}y}{dx^{2}}$ if y^2-x^2 = 4 .

Possible Answers:

$\frac{x}{\sqrt{4+x^2}}$

$\frac{x^2-4}{\sqrt{x^2+4}}$

$\frac{x^2}{(x^2-4)^\frac{3}{2}}$

$\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$

$\frac{x^2+4}{(x^2-4)^\frac{3}{2}}$

Correct answer:

$\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$

Explanation:

We will have to find the first derivative of with respect to using implicit differentiation. Then, we can find $\frac{d^{2}y}{dx^{2}}$ , which is the second derivative of with respect to .

$\frac{d}{dx}[y^2-x^2]=\frac{d}{dx}[4]$

We will apply the chain rule on the left side.

$\frac{d}{dx}[y^2]\cdot \frac{dy}{dx}-\frac{d}{dx}[x^2]=0$

$2y\cdot \frac{dy}{dx}-2x=0$

We now solve for the first derivative with respect to .

$\frac{dy}{dx}=\frac{x}{y}$

In order to get the second derivative, we will differentiate $\frac{x}{y}$ with respect to . This will require us to employ the Quotient Rule.

$\frac{d}{dx}\frac{dy}{dx}=\frac{d^{2}y}{dx^{2}}=\frac{d}{dx}[\frac{x}{y}]=\frac{y\cdot \frac{d}{dx}[x]-x\cdot \frac{d}{dx}[y]}{y^{2}} =\frac{y\cdot 1-x\cdot \frac{dy}{dx}}{y^{2}}$

We will replace $\frac{\mathrm{d}y }{\mathrm{d} x}$ with $\frac{x}{y}$ .

$\frac{y-x(\frac{x}{y})}{y^{2}}=\frac{y^{2}-x^{2}}{y^{3}}$

But, from the original equation, $y^{2}-x^{2}=4$ . Also, if we solve for , we obtain $y = (4+x^{2})^{\frac{1}{2}}$ .

$\frac{d^{2}y}{dx^{2}}=\frac{y^{2}-x^{2}}{y^{3}}=\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$

The answer is $\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$ .

Report an Error

Example Question #3 : Understanding The Limiting Process.

Differentiate f(x)=5x^3 .

Possible Answers:

15x^2

15x^3

15x^4

(5/3)x^2

8x^2

Correct answer:

15x^2

Explanation:

Using the power rule, multiply the coefficient by the power and subtract the power by 1.

f(x)=5x^3

$f'(x)=5*3(x^{3-1})$

f'(x)=15x^2

Report an Error

Example Question #4 : Understanding The Limiting Process.

Differentiate $f(x)=\frac{1}{x^2}$ .

Possible Answers:

$\frac{-2}{x}$

$\frac{-2}{x^3}$

$\frac{1}{x^3}$

2ln(x^2)

ln(x^2)

Correct answer:

$\frac{-2}{x^3}$

Explanation:

Use the product rule:

$f(x)=\frac{1}{x^2}= x^{-2}$

$f'(x)=-2*1(x^{-2-1})= {-2}*{x^{-3}}= \frac{-2}{x^3}$

Report an Error

View AP Calculus AB Tutors

Vikash
Certified Tutor

national institute of technology Jamshedpur , Bachelor, Civil engineering .

View AP Calculus AB Tutors

Rohan
Certified Tutor

Purdue University-Main Campus, Bachelor of Engineering, Aerospace Engineering.

View AP Calculus AB Tutors

Angela
Certified Tutor

Saint Josephs College, Bachelor in Arts, Mathematics.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Los Angeles, Computer Science Tutors in Miami, ISEE Tutors in Philadelphia, ACT Tutors in Seattle, Biology Tutors in Seattle, ACT Tutors in Phoenix, SSAT Tutors in San Diego, Biology Tutors in Philadelphia, Math Tutors in Miami, ACT Tutors in Philadelphia

Popular Courses & Classes

Spanish Courses & Classes in Houston, MCAT Courses & Classes in Houston, GRE Courses & Classes in New York City, LSAT Courses & Classes in Phoenix, Spanish Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Seattle, LSAT Courses & Classes in Boston, LSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Atlanta

Popular Test Prep

LSAT Test Prep in San Diego, GRE Test Prep in Philadelphia, ISEE Test Prep in Miami, ISEE Test Prep in Chicago, GRE Test Prep in New York City, LSAT Test Prep in Philadelphia, MCAT Test Prep in Philadelphia, LSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in San Francisco-Bay Area, SAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Functions, Graphs, and Limits

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #33 : Limits Of Functions (Including One Sided Limits)

Example Question #172 : Functions, Graphs, And Limits

Example Question #1 : Understanding The Limiting Process.

Example Question #1 : Understanding The Limiting Process.

Example Question #2 : Understanding The Limiting Process.

Example Question #35 : Limits Of Functions (Including One Sided Limits)

Example Question #4 : Understanding The Limiting Process.

Example Question #4 : Calculus 3

Example Question #3 : Understanding The Limiting Process.

Example Question #4 : Understanding The Limiting Process.

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: