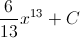Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Asymptotic and Unbounded Behavior

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int\frac{1}{x^2}dx$

Possible Answers:

3x^3+C

$-x^{-1}+C$

$\frac{-1}{3x^3}+C$

(1/2)ln(x)+C

2ln(x)+C

Correct answer:

$-x^{-1}+C$

Explanation:

We evaluate the integral according to this equation:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C, n\ne1$ . From this, we acquire the answer above. Keep in mind that $\frac{1}{x^{2}}$ is the same as $x^{-2}$ . As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #47 : Functions, Graphs, And Limits

Evaluate the following indefinite integral.

$\int(3x^7+4x^4)dx$

Possible Answers:

8x^8+5x^5+C

3x^6+4x^3+C

$\frac{3}{8}x^8+\frac{4}{5}x^5+C$

$\frac{1}{8}x^8+\frac{1}{5}x^5+C$

$\frac{8}{3}x^8+\frac{5}{4}x^5+C$

Correct answer:

$\frac{3}{8}x^8+\frac{4}{5}x^5+C$

Explanation:

First, we remember that the integral of a sum is the same as the sum of the integrals, so we can split the sum into seperate integrals and solve them individually. We then evaluate each integral according to this equation:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C, n\ne1$ . From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #251 : Ap Calculus Ab

Evaluate the following indefinite integral.

$\int\frac{1}{2}x^2dx$

Possible Answers:

$\frac{1}{2}x^3+C$

$\frac{1}{6}x^3+C$

$\frac{1}{2}x^3+C$

3x^3+C

6x^3+C

Correct answer:

$\frac{1}{6}x^3+C$

Explanation:

First, we know that we can pull the constant $\frac{1}{2}$ out of the integral, and we then evaluate the integral according to this equation:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C, n\ne1$ . From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #49 : Functions, Graphs, And Limits

Evaluate the following indefinite integral.

$\int \frac{3}{5}x^3dx$

Possible Answers:

$\frac{3}{20}x^4+C$

$\frac{9}{5}x^4+C$

$\frac{3}{15}x^4+C$

$\frac{1}{20}x^4+C$

$\frac{20}{3}x^4+C$

Correct answer:

$\frac{3}{20}x^4+C$

Explanation:

First, we know that we can pull the constant $\frac{3}{5}$ out of the integral, and we then evaluate the integral according to this equation:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C, n\ne1$ . From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #252 : Ap Calculus Ab

Evaluate the following indefinite integral.

$\int\sqrt{x}dx$

Possible Answers:

ln(x)+C

$\frac{2}{3}x^{\frac{3}{2}}+C$

e^x+C

$3x^{-1/2}+C$

$\frac{1}{3}x^{\frac{1}{2}}+C$

Correct answer:

$\frac{2}{3}x^{\frac{3}{2}}+C$

Explanation:

We evaluate the integral according to this equation:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C, n\ne1$ . Keep in mind that $\sqrt{x}$ is the same as $x^{1/2}$ . From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #253 : Ap Calculus Ab

Evaluate the following indefinite integral.

$\int2e^{2x}dx$

Possible Answers:

e^x+C

$\frac{1}{2}e^{2x}+C$

$e^{2x}+C$

$\frac{1}{2}e^x+C$

2e^x+C

Correct answer:

$e^{2x}+C$

Explanation:

We know that the derivative of $e^{x}=e^{x}$ and the integral of $e^{x}=e^{x}$ . We must remember the chain rule and therefore keep the 2 in the exponent. From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #41 : Asymptotic And Unbounded Behavior

Evaluate the following indefinite integral.

$\int\frac{1}{6}x^{12}dx$

Possible Answers:

$\frac{6}{13}x^{13}+C$

$2x^{13}+C$

$72x^{13}+C$

$\frac{1}{78}x^{13}+C$

$2x^{11}+C$

Correct answer:

$\frac{1}{78}x^{13}+C$

Explanation:

First, we know that we can pull the constant $\frac{1}{6}$ out of the integral, and we then evaluate the integral according to this equation:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C, n\ne1$ . From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #261 : Ap Calculus Ab

Evaluate the following indefinite integral.

$\int e^xdx$

Possible Answers:

$e^{-x}+C$

1/ln(x)+C

ln(x)+C

e^x+C

$\frac{1}{2}e^{-x}+C$

Correct answer:

e^x+C

Explanation:

For this problem, we must simply remember that the integral of $e^{x}$ is $e^{x}$ , just like how the derivative of $e^{x}$ is $e^{x}$ . Just keep in mind that we need that constant of integration that would have been lost during differentiation.

Report an Error

Example Question #21 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int 3y^2 dy$

Possible Answers:

6y^3+C

y^3+C

$\frac{1}{3}y^3+C$

$\frac{3}{2}y^3+C$

$\frac{2}{3}y^3+C$

Correct answer:

y^3+C

Explanation:

First, we know that we can pull the constant out of the integral, and we then evaluate the integral according to this equation:

$\int y^n dy=\frac{y^{n+1}}{n+1}+C, n\ne1$ . From this, we acquire the answer above. As a note, we cannot forget the constant of integration which would be lost during the differentiation.

Report an Error

Example Question #41 : Asymptotic And Unbounded Behavior

$\int \sec x\tan x\ \mathrm{d}x=$

Possible Answers:

$\frac{1}{2}sec^2xtanx +C$

tan(x)sec(x)

sec(x)+C

tan(x)+C

-tan(x)+C

Correct answer:

sec(x)+C

Explanation:

The answer is sec(x)+C . The definition of the derivative of sec(x) is sec(x)tan(x) . Remember to add the to undefined integrals.

Report an Error

View AP Calculus AB Tutors

Blake
Certified Tutor

Vanderbilt University, Bachelors, Neuroscience.

View AP Calculus AB Tutors

Siddharth
Certified Tutor

University of Petroleum and Energy Studies and, Masters in Business Administration, Aviation Management.

View AP Calculus AB Tutors

Andrew
Certified Tutor

University of Wisconsin-Stevens Point, Bachelor of Science, Mathematics. University of Wisconsin-Oshkosh, Master of Science, ...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Dallas Fort Worth, Calculus Tutors in Boston, Calculus Tutors in San Diego, Physics Tutors in Dallas Fort Worth, SSAT Tutors in Philadelphia, Math Tutors in Washington DC, French Tutors in New York City, English Tutors in Chicago, SSAT Tutors in Seattle, Algebra Tutors in Seattle

Popular Courses & Classes

GMAT Courses & Classes in Miami, GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Chicago, MCAT Courses & Classes in San Diego, GRE Courses & Classes in Atlanta, GRE Courses & Classes in New York City, GMAT Courses & Classes in San Diego, MCAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Philadelphia, SAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, GMAT Test Prep in Seattle, GMAT Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth, SSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Los Angeles, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Asymptotic and Unbounded Behavior

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #11 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #47 : Functions, Graphs, And Limits

Example Question #251 : Ap Calculus Ab

Example Question #49 : Functions, Graphs, And Limits

Example Question #252 : Ap Calculus Ab

Example Question #253 : Ap Calculus Ab

Example Question #41 : Asymptotic And Unbounded Behavior

Example Question #261 : Ap Calculus Ab

Example Question #21 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #41 : Asymptotic And Unbounded Behavior

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: