All AP Calculus AB Resources
Example Questions
Example Question #81 : Applications Of Derivatives
Find 
To find 
Taking 
using the following rules:



Note that for every derivative of a function with y, the additional term 
Using algebra to solve for 

Example Question #82 : Applications Of Derivatives
Use implicit differentiation to calculate the equation of the line tangent to the equation 
Differentiate both sides of the equation:
Simplify:
Use implicit differentiation to differentiate the y term:
Subtract 4x from both sides of the equation:
Divide both sides of the equation by 2y:
Plug in the appropriate values for x and y to find the slope of the tangent line:
Use slope-intercept form to solve for the equation of the tangent line:
Plug in the appropriate values of x and y into the equation, to find the equation of the tangent line:
Solve for b:
Solution:
Example Question #83 : Applications Of Derivatives
Find 

To find 
Taking 
and the derivatives were found using the following rules:



Note that for every derivative of a function with z, the additional term 
Using algebra to solve, we get
Example Question #84 : Applications Of Derivatives
Find the normal line of the curve 
Use implicit differentiation to calculate the slope of the tangent line:
Simplify:
Subtract x from both sides of the equation:
Divide both sides of the equation by 2y:
Plug in the x and y values from the point 
Take the negative reciprocal of the slope of the tangent line to calculate the slope of the normal line:
Plug the slope of the normal line into point slope form:
Add 
Simplify the equation:
Simplify further:
Solution:
Example Question #671 : Derivatives
Find 

To find the derivative at 

Plugging in 
Example Question #672 : Derivatives
Find the derivative of the following function at the point 
Use the power rule on each term of the polynomial to get the derivative,
Now we plug in
Example Question #2091 : High School Math
Let 

We need to find the first derivative of f(x). This will require us to apply both the Product and Chain Rules. When we apply the Product Rule, we obtain:
In order to find the derivative of 
We can factor out a 2x to make this a little nicer to look at.
Now we must evaluate the derivative when x = 
The answer is 
Certified Tutor
Certified Tutor
All AP Calculus AB Resources











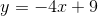
























































![f'(x)=\sin(x^2)\cdot\frac{\mathrm{d} }{\mathrm{d} x}[x^2]+x^2\cdot\frac{\mathrm{d} }{\mathrm{d} x}[\sin(x^2)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/109754/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[\sin(x^2)]=\cos(x^2)\cdot\frac{\mathrm{d} }{\mathrm{d} x}[x^2]=\cos(x^2)\cdot2x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/128240/gif.latex)







