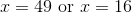One way to solve this equation is to substitute $\displaystyle u$ for $\displaystyle \sqrt{x}$ and, subsequently, $\displaystyle u^{2}$ for $\displaystyle x$:

$\displaystyle x + 3 \sqrt{x} = 28$

$\displaystyle u^{2} + 3 u = 28$

$\displaystyle u^{2} + 3 u - 28 = 0$

Solve the resulting quadratic equation by factoring the expression:

$\displaystyle (u+7)(u-4) = 0$

Set each linear binomial to sero and solve:

$\displaystyle u + 7 = 0$

$\displaystyle u = -7$

or 

$\displaystyle u - 4 = 0$

$\displaystyle u = 4$

Substitute back:

$\displaystyle u = -7$

$\displaystyle \sqrt{x}= -7$ - this is not possible.

$\displaystyle u = 4$

$\displaystyle \sqrt{x}= 4$

$\displaystyle x = 16$ - this is the only solution.

None of the responses state that $\displaystyle x = 16$ is the only solution.

We can simplify the fraction:

$\displaystyle \frac{10\sqrt{8}}{\sqrt{16}} = \frac{10\sqrt{4\times 2}}{4}=\frac{10(2\sqrt{2})}{4} =\frac{20\sqrt{2}}{4}=5\sqrt{2}$

Plugging this into the equation leaves us with:

$\displaystyle 5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}$ 

Note: Because they are like terms, we can add them.

In order to solve this equation, we need to know that

             $\displaystyle (\sqrt{x-6})^{2} = x-6$

How? Because of these two facts: 

1. $\displaystyle \sqrt{x-6} = (x-6)^{\frac{1}{2}}$
2. Power rule of exponents: when we raise a power to a power, we need to mulitply the exponents:

                                      $\displaystyle \frac{1}{2} \times2=1$

With this in mind, we can solve the equation:

$\displaystyle \sqrt{x-6} =2$

In order to eliminate the radical, we have to square it. What we do on one side, we must do on the other.

$\displaystyle (\sqrt{x-6})^{2} = 2^{2}$

$\displaystyle x-6=4$

$\displaystyle x=10$

In order to solve this equation, we need to know that 

 $\displaystyle \bigg(\sqrt{\frac{x}{2}}\bigg)^{2} =\frac{x}{2}$

Note: This is due to the power rule of exponents.

With this in mind, we can solve the equation:

$\displaystyle \sqrt{\frac{x}{2}} =5$

In order to get rid of the radical we square it. Remember what we do on one side, we must do on the other.

$\displaystyle \bigg(\sqrt{\frac{x}{2}}\bigg)^{2} =5^{2}$

$\displaystyle \frac{x}{2} =25$

$\displaystyle \frac{2}{1} \bigg(\frac{x}{2}\bigg)=25\bigg(\frac{2}{1}\bigg)$

$\displaystyle x=50$

To solve, perform inverse opperations, keeping in mind order of opperations:

$\displaystyle \sqrt{2x+1} = 11$ first, square both sides

$\displaystyle 2x + 1 = 121$ subtract 1

$\displaystyle 2x = 120$ divide by 2 

$\displaystyle x = 60$

To solve, perform inverse opperations, keeping in mind order of opperations:

$\displaystyle (\sqrt x + 19 ) ^ 2 = 10,000$ take the square root of both sides

$\displaystyle \sqrt x + 19 = 100$ subtract 19 from both sides

$\displaystyle \sqrt{x } = 81$ square both sides

$\displaystyle x = 6,561$

To solve, use inverse opperations keeping in mind order of opperations:

$\displaystyle 5\sqrt {x-12} = 20$ divide both sides by 5

$\displaystyle \sqrt{x-12 } = 4$ square both sides

$\displaystyle x - 12 = 16$ add 12 to both sides

$\displaystyle x = 28$

$\displaystyle \sqrt{x}=4$ To get rid of the radical, we square both sides.

$\displaystyle x=4^2=16$

To get rid of the radical, we need to square both sides. The issue is radicals don't generate negative numbers unless we talk about imaginary numbers. In this case, our answer choice should be no answer. 

$\displaystyle \sqrt{x+1}=5$ Square both sides to get rid of the radical.

$\displaystyle x+1=5^2=25$ Subtract $\displaystyle 1$ on both sides.

$\displaystyle x=24$