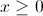The first step is to distribute (multiply) through the parentheses:

Then subtract  from both sides of the inequality:

Next, subtract the 12:

Finally, divide by two:

First, we determine the equation of the boundary line. This line includes points  and  , so the slope can be calculated as follows:

Since we also know the -intercept is , we can substitute  in the slope-intercept form to obtain equation of the boundary:

The boundary is included, as is indicated by the line being solid, so the equality symbol is replaced by either  or . To find out which one, we can test a point in the solution set - for ease, we will choose :

 _____   

  _____ 

  _____ 

0 is less than 7 so the correct symbol is . 

The correct choice is .

First, add 2 to both sides of the inequality:

 and simplify: .

Then, multiply each side by 3: 

 and simplify: . 

Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that  becomes , and vice versa.

To make this problem easier to solve, we can add 2 to both sides so that we can factor the left side of the expression.

The breakpoints to examine are at 

These two breakpoints create 3 total regions that we need to examine:

, , and . Which ever region satisfies the expression above will be a solution to the inequality.

A value of -3 gives us: .

 is greater than 0, so it satisfies the inequality.

A value of -1.5 for the second region does not satisfy the inequality.

A value of 0 for the third region does satify the inequality, so the first and third regions give us our answer.

.

When solving an inequality, first isolate the variable: 

(subtract 5 from both sides)

___________________

(divide both sides by -2)

(remember when dividing both sides by a negative, you must flip the inequality sign because the sign on both sides changed)

 is the answer! 

Important note:

The negative two cancels on the right side and the  on the left side. Since both sides went from negative to positive values the inequality sign flips.

Isolate all the terms with x on one side and all other terms on the other side. Our first step is to subtract four from each side.

We the get

.

We now need to divide both sides by -5.

However, whenever you multiply or divide by a negative number, you flip the direction of the inequality.

To solve the inequality we want to isolate the x variable on one side and all other constants on the other side.

The first step is two add six to both sides.

Next, divide by negative four and remember when dividing by a negative you must flip the inequality sign.

To solve absolute value inequalities, you have to set up two different inequalities: and . Then, solve each one separately as normal. The first one yields a solution set of and the second one yields . Those are your two answers.