Algebra II : Scatter Plots
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #1 : Construct And Interpret Scatter Plots: Ccss.Math.Content.8.Sp.A.1
Which of the following would most likely represent an outlier on a scatterplot which relates height (in inches) to shoe size for men?
An outlier is defined as a point that does not fit within the general pattern of the data. Thus, we are looking for a height that is not within the normal range for an adult male, and shoe size which is outside of the range for an adult male. Typically, an adult male would be between 65 and 77 inches tall (5 feet 5 inches and 6 feet 5 inches). Typically, an adult male's shoe size would be around a 10. Thus, the outlier would have height and shoe size drastically different from these, 
Example Question #2 : Construct And Interpret Scatter Plots: Ccss.Math.Content.8.Sp.A.1
Which of the following represents a positive association in a scatterplot?
As 
There is no pattern amongst the data.
As 
As 
As 
As
A positive association is defined as a scatterplot on which the best fit line has a positive slope.
This pattern is identified because on the graph, looking from left to right, the vast majority of the points goes up.
This can also be described by saying, "as 
Example Question #1 : Scatter Plots
A scatterplot correlates adult males' height vs. shoe size. What does the point 
One adult male who is 72 inches tall and with a shoe size of 13.
The median adult male height and shoe size.
That 72 inches and 13 shoe size are outliers compared to the rest of the adult male population.
The mean adult male height and shoe size.
All adult males that were surveyed were the same height and weight.
One adult male who is 72 inches tall and with a shoe size of 13.
When creating a scatterplot, data is collected. This data is formulated into ordered pairs. Each of these ordered pairs, which are later graphed, represent one person's data. Thus, this particular piece of data would represent one man's height of 
Example Question #1 : Scatter Plots
What would be the most accurate line of best fit for this scatter plot?
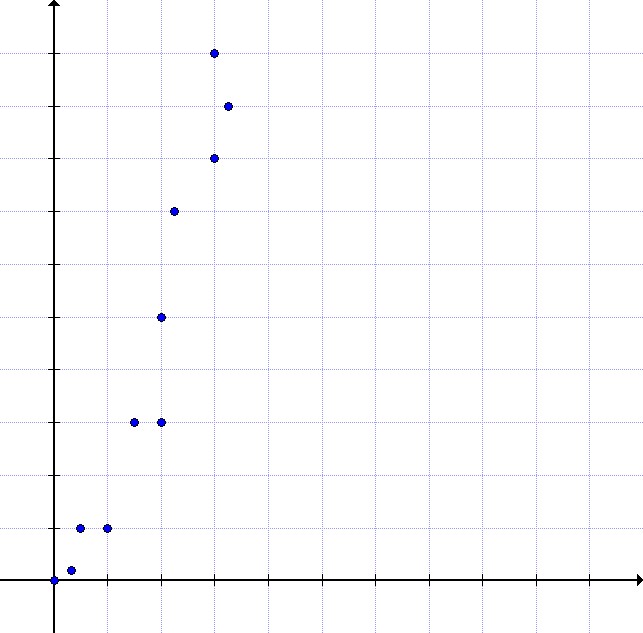
This data is quadratic rather than linear - it increases much more sharply than the line 
Example Question #1 : Construct And Interpret Scatter Plots: Ccss.Math.Content.8.Sp.A.1
What type of correlation does this data have?
Negative correlation
Linear correlation
Positive correlation
No correlation
Positive correlation
It has a positive correlation because the points all trend upward. In other words, as the independent variable on the x-axis increases, the dependent variable on the y-axis also increases. Therefore, the line of best fit that is drawn through the data represents a positive line as it has a positive slope. This verifies that our data has a positive correlation.
Example Question #1 : Scatter Plots
This scatter plot represents data about snack quality (
I. The price of a higher quality snack tends to be higher.
II. Points below the line represent snacks whose price is higher than their quality.
III. Points above the line represent snacks whose quality is higher than their price.
II only
I and II
I and III
I only
I only
I. is a true statement about the scatter plot: as quality increases, price tends to increase.
II. is not true - the points under the line have a relatively low price compared to their quality.
III. is also not true - the points above the line have relatively low quality compared to their price.
Certified Tutor
All Algebra II Resources
