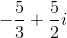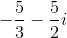Simplify the complex fraction by first rewriting the expression using a division sign.

Multiply and reduce the fractions.

Add four to this fraction.

The answer is:  

Simplify each complex fraction using the multiplication rule of dividing fractions.

Divide the fractions.

Reduce the fractions.

The answer is:  

Simplify the complex fraction first.  Rewrite it using a division sign.

We can change the division sign to a multiplication sign and take the reciprocal of the second fraction.

Replace this fraction as the second fraction.

Apply the same rule for these fractions.

The answer is:  

Simplify each complex fraction by using the multiplicative rule of division.

Rewrite each term using a division sign and simplify by changing the division sign to a multiplication sign, and take the reciprocal of the second term.

Rewrite the fractions.

Repeat the process for these fractions.

The answer is:   

In order to divide the two fractions, we will need to change the division sign to multiplication, and take the reciprocal of the right side.

The answer is:  

1) In order to multiply fractions you first want multiply the two numerators together which will give you the multiplied numerator.

 This gives you a multiplied numerator of .

2) Next you should do the same time to the denominator, which will give you the multiplied numerator. Unlike addition or subtraction of fractions you do not need to find a common denominator.

3) Putting the results together for numerators and denominators it becomes , however you are not done with this problem, as the answer isn't fully simplified. In order to simplify it look for common factors in the numerator. The easiest way is to check if both the numerators are even numbers, in which case they are both divisible by .

In this case both the numerator and denominator are divisible by 2 so you it can be reduced to .

4) Once you simplify the expression ask once more if the expression can be simplified more, as often times, including this case, it can be. Here you have a  in the numerator and a  in the denominator. Ask "what are both  and  divisible?" They are divisible by  as well, but the simpler method would be divide them both by  as they're both divisible by . Since this produces a  in the numerator you are now done simplifying and your final answer is .

Use the FOIL technique:

To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem,  is our denominator, so we will multiply the expression by  to obtain:

.

We can then combine like terms and rewrite all  terms as . Therefore, the expression becomes:

Our final answer is therefore 

Multiply these complex numbers out in the typical way:

and recall that  by definition. Then, grouping like terms we get

which is our final answer.