All Algebra II Resources
Example Questions
Example Question #81 : Inverse Functions
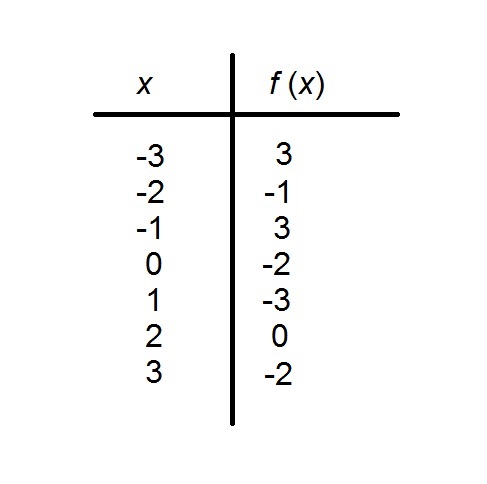
The above table shows a function with domain 
True or false: 
False
True
False
A function 




If we order the rows by range value, we see this to not be the case:



Example Question #82 : Inverse Functions
Define a function 
Which statement correctly gives 
None of these
The inverse function 

Replace 

Switch the positions of 


Solve for 
First, subtract 15:
Multiply by 
Distribute:
Replace 


the correct response.
Example Question #83 : Inverse Functions
Define a function 
Which statement correctly gives 
The inverse function 

Replace 

Switch the positions of 


or
Solve for 
Square both sides:
Add 5 to both sides:
Multiply both sides by 
Replace 


the correct response.
Example Question #84 : Inverse Functions

Above is the graph of a function 







Given the graph of 



The figure in blue is the graph of
Example Question #85 : Inverse Functions

Which of the following is true of the graphed relationship?
None of these
The relation is a function, and it has an inverse.
All of these
The relation is not a function.
The relation is a function, but it does not have an inverse.
The relation is a function, and it has an inverse.
A relation is a function if and only if it passes the Vertical Line Test (VLT) - that is, no vertical line exists that passes through its graph more than once. From the diagram below, we see that no such line exists:

The relation passes the VLT, so it is a function.
A function has an inverse if and only if it passes the Horizontal Line Test (HLT) - that is, no horizontal line exists that passes through its graph more than once. From the diagram below, we see that no such line exists:

The function passes the HLT, so it has an inverse.
Example Question #86 : Inverse Functions
Define a function 
Which statement correctly gives 
None of these
The inverse function 

Replace 

Switch the positions of 

or
Solve for 
Raise 
A property of logarithms states that 
Subtract 7 from both sides:
Multiply both sides by 
Replace 

Example Question #87 : Inverse Functions

Which of the following is true regarding the relation in the provided graph?
None of these
The relation is a function, and it has an inverse.
The relation is a function, and it has more than one inverse.
The relation is not a function.
The relation is a function, but it does not have an inverse.
The relation is a function, but it does not have an inverse.
A relation is a function if and only if it passes the Vertical Line Test (VLT)—that is, no vertical line exists that passes through its graph more than once. From the diagram below, we see that no such line exists:

A function has an inverse, if and only if, it passes the Horizontal Line Test (HLT) - that is, no horizontal line exists that passes through its graph more than once. From the diagram below, we see at least one such line exists.

The function fails the HLT, so it does not have an inverse.
Example Question #88 : Inverse Functions

Define a function 

Which table correctly gives 






One definition of the inverse function 







or, ordering the 

Example Question #89 : Inverse Functions

Which of the following is true of the relation present in the provided graph?
None of these
The relation is a function, but it does not have an inverse.
The relation is not a function.
The relation is a function, and it has an inverse.
The relation is not a function but has an inverse.
The relation is a function, and it has an inverse.
A relation is a function, if and only if, it passes the Vertical Line Test (VLT)—that is, no vertical line exists that passes through its graph more than once. From the diagram below, we see that no such line exists:

The relation passes the VLT, so it is a function.
A function has an inverse if and only if it passes the Horizontal Line Test (HLT) - that is, no horizontal line exists that passes through its graph more than once. From the diagram below, we see that no such line exists:

The function passes the HLT, so it has an inverse.
Example Question #90 : Inverse Functions

Which of the following is true of the relation graphed above?
The relation is a function, but it does not have an inverse.
The relation is not a function but it has an inverse.
None of these
The relation is not a function.
The relation is a function, and it has an inverse.
The relation is a function, but it does not have an inverse.
A relation is a function, if and only if, it passes the Vertical Line Test (VLT)—that is, no vertical line exists that passes through its graph more than once. From the diagram below, we see that no such line exists;

The relation passes the VLT, so it is a function.
A function has an inverse if and only if it passes the Horizontal Line Test (HLT) - that is, no horizontal line exists that passes through its graph more than once. From the diagram below, we see at least one such line exists.

The function fails the HLT, so it does not have an inverse.
Certified Tutor
All Algebra II Resources














































