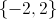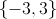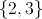The correct answer is . Because the constant is negative, the answer must contain terms with positive and negative constants, thus ruling out , which would result in a positive coefficient. The   answer choice can be ruled out because the factored out polynomial results in a , not a . Therefore, the correct answer choice is, which can be confirmed if multiplied out. 

This problem is an example of a difference of squares. The formula for such a problem is . In this problem  corresponds to  and  corresponds to . Therefore, the solution is . 

When working with problems like these, you want to put the monomials in a standard format with the highest ordered terms on the left. 

So the denominator should read: 

The entire expression will then read: 

Then factor out a  from the equation so it reads 

The like terms then cancel leaving . 

By substituting  - and, subsequently,  this can be rewritten as a quadratic equation, and solved as such:

We are looking to factor the quadratic expression as , replacing the two question marks with integers with product  and sum 5; these integers are .

Substitute back:

The first factor cannot be factored further. The second factor, however, can itself be factored as the difference of squares:

Set each factor to zero and solve:

Since no real number squared is equal to a negative number, no real solution presents itself here. 

The solution set is .

Rewriting the equation as , we can see there are four terms we are working with, so factor by grouping is an appropriate method. Between the first two terms, the Greatest Common Factor (GCF) is  and between the third and fourth terms, the GCF is 4. Thus, we obtain .   Setting each factor equal to zero, and solving for , we obtain  from the first factor and  from the second factor. Since the square of any real number cannot be negative, we will disregard the second solution and only accept . 

The first step is to determine if all of the terms have a greatest common factor (GCF). Since a GCF does not exist, we can move onto the next step.

Create smaller groups within the expression. This is typically done by grouping the first two terms and the last two terms.

Factor out the GCF from each group:

At this point, you can see that the terms inside the parentheses are identical, which means you are on the right track!

Since there is a GCF of (5x+1), we can rewrite the expression like this:

And that is your answer! You can always check your factoring by FOILing your answer and checking it against the original expression.

This can be most easily solved by setting  and, subsequently, . This changes the degree-4 polynomial in  to one that is quadratic in , which can be solved as follows:

The quadratic factors do not fit any factoring pattern and are prime, so this is as far as the polynomial can be factored.

To find , we must start inwards and work our way outwards, i.e. starting with :

We can now use this value to find  as follows:

Our final answer is therefore 

Using the difference of cubes formula:

Find x and y:

Plug into the formula:

Which Gives:

And cannot be factored more so the above is your final answer.

First, we can factor a  from both terms:

Now we can make a clever substitution.  If we make  the function now looks like:

This makes it much easier to see how we can factor (difference of squares):

The last thing we need to do is substitute  back in for , but we first need to solve for  by taking the square root of each side of our substitution:

Substituting back in gives us a result of: