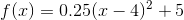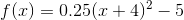Algebra II : Functions and Graphs
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #181 : Functions And Graphs
Which of the following represents a standard parabola shifted up by 2 units?
Begin with the standard equation for a parabola: 
Vertical shifts to this standard equation are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift upward 2 units, add 2.
Example Question #4 : Transformations
Which of the following transformation flips a parabola vertically, doubles its width, and shifts it up by 3?
Begin with the standard equation for a parabola: 
Inverting, or flipping, a parabola refers to the sign in front of the coefficient of the 
The width of the parabola is determined by the magnitude of the coefficient in front of 
Vertical shifts are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift upward 3 units, add 3.
Example Question #5 : Transformations
Which of the following shifts a parabola six units to the right and five downward?
Begin with the standard equation for a parabola:
Vertical shifts to this standard equation are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift downward 5 units, subtract 5.
Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the 
Example Question #6 : Transformations
Which of the following transformations represents a parabola that has been flipped vertically, shifted to the right 12, and shifted downward 4?
Begin with the standard equation for a parabola:
Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the 
Inverting, or flipping, a parabola refers to the sign in front of the coefficient of the 
Vertical shifts are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift downward 4 units, subtract 4.
Example Question #7 : Transformations
Which of the following transformations represents a parabola that has been shifted 4 units to the left, 5 units down, and quadrupled in width?
Begin with the standard equation for a parabola:
Horizontal shifts are represented by additions (leftward shifts) or subtractions (rightward shifts) within the parenthesis of the 
The width of the parabola is determined by the magnitude of the coefficient in front of 
Vertical shifts are represented by additions (upward shifts) or subtractions (downward shifts) added to the end of the equation. To shift downward 5 units, subtract 5.
Example Question #1 : Transformations
If the function 
Shifting 
The new equation after shifting left 2 units is:
Shifting up 3 units will add 3 to the y-intercept of the new equation.
The answer is:
Example Question #1 : Transformations
If 
It is the same as 
It is the 
It is the 
It is the 
It is the 
It is the
It helps to evaluate the expression algebraically.
This is the graph of
and this is the graph of
Example Question #10 : Transformations
If 
It is the 
It is the 
It is the 
It is the 
It is the 
It is the
Algebraically, 
This is a reflection across the y axis.
This is the graph of
And this is the graph of
Example Question #11 : Transformations
Transformations
Where will the point 
- Reflection about the x-axis
- Translation up 3
- Translation right 4
Where will the point 
- Reflection about the x-axis results in multiplying the y value by negative one thus
.
- Translation up 3, means to add three to the y values which results in
.
- Translation right 4, means to add four to the x value which will result in
.
Example Question #12 : Transformations
Find the equation of the linear function 
y-intercept
y-intercept
y-intercept
y-intercept
y-intercept
y-intercept
The transformation for a left shift along the x-axis for 
The y-intercept of the linear function 
All Algebra II Resources
