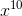We begin by distributing the power to all terms within the parentheses. Remember that when we raise a power to a power, we multiply each exponent:

Anytime we have negative exponents, we can convert them to positive exponents. However, if the exponent was negative in the numerator, the term shifts to the denominator. If the exponent was negative in the denominator, the term shifts to the numerator. 

To simplify this, we will need to use the power rule and order of operations.

Evaluate the first term.  This will be done in two ways to show that the power rule will work for exponents outside of the parenthesis for a single term.

For the second term, we cannot distribute  and  with the exponent  outside the parentheses because it's not a single term.  Instead, we must evaluate the terms inside the parentheses first.

 Evaluate the second term.

Square the value inside the parentheses.

Subtract the value of the second term with the first term.

First convert  into a known base.  The number  can be rewritten as .

Rewrite the expression.

Use the power rule to multiply the exponents.

Use order of operations to evaluate the expression.

Which of the following is equivalent to the expression ?

We can rewrite the given expression by distributing the exponent on the outside.

Now, this may look a little messier, but we need to recall that when we distribute an exponent through parentheses as we are trying to do above, we need to multiple the exponent on the inside by the number on the outside. 

In a general sense it looks like this:

For our specific problem, it looks like this:

To simplify this expression, recall that it could be written as this: . Since we're dealing with a quartic root, for every 4 of the same term, cross them out underneath the radical and bring one of those terms out. Therefore, we are only left with one x underneath the radical. The answer is: .

Simplify the following expression:

To raise exponents to another power, we need to multiply them:

So we get:

Simplify the following expression:

To simplify exponents that are being raised to a higher power, we need to multiply each term's exponent by the exponent outside of the parentheses.

Follow up by actually multiplying through

Making our answer:

Simplify the following expression by distributing the exponent:

When we are distributing an exponent, we want to multiple the exponent of each term within the parentheses by the exponent outside the parentheses.

Finally, perform the multiplication to get your answer:

When an exponent is being raised by another exponent, we just multiply the powers of the exponents and keep the base the same.

When an exponent is being raised by another exponent, we just multiply the powers of the exponents and keep the base the same.