All Algebra II Resources
Example Questions
Example Question #25 : Functions And Graphs

The above table refers to a function 

Is this function even, odd, or neither?
Cannot be determined
Odd
Neither
Even
Even
A function 




Of course,

Therefore, 
Example Question #28 : Functions And Graphs
Which of the following equations is that of an oblique asymptote of the graph of the function 
The graph of 
To find an oblique asymptote of a rational function whose numerator has higher degree than its denominator, as is the case here, divide the former by the latter, as follows:

Divide the leading term of the dividend by that of the divisor:
Place this in the quotient, and multiply this by the divisor:
Subtract this from the dividend. The figure should look like this:

Repeat with the difference:
The figure now looks like this:

The difference has degree less than that of the divisor, so the division is finished. The oblique asymptote is the quotient,
Example Question #1 : Understanding Domain And Range
Domain: All real numbers
Range:
Domain: All real numbers
Range:
Domain: All real numbers
Range:
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 


Example Question #1 : Domain And Range
Which of the following is NOT a function?
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












Example Question #3 : How To Find The Domain Of A Function
Give the domain of the function below.

The domain is the set of possible value for the 

Now we can solve for 
There is no real value of 
The radicand is always positive, and 


Example Question #3 : How To Factor The Quadratic Equation
Find the domain:
To find the domain, find all areas of the number line where the fraction is defined.

Factor by finding two numbers that sum to -2 and multiply to 1. These numbers are -1 and -1.
Example Question #3 : How To Find The Domain Of A Function
What is the domain of the function 
The domain is the set of x-values that make the function defined.
This function is defined everywhere except at 
Example Question #3 : Functions And Graphs
If 

Using 



Therefore 

Example Question #32 : Functions And Graphs
What is the range of the function?
This function is a parabola that has been shifted up five units. The standard parabola has a range that goes from 0 (inclusive) to positive infinity. If the vertex has been moved up by 5, this means that its minimum has been shifted up by five. The first term is inclusive, which means you need a "[" for the beginning.
Minimum: 5 inclusive, maximum: infinity
Range:
Example Question #3 : Functions And Graphs
What is the domain of the function?
The domain represents the acceptable 
Minimum: 0 inclusive, maximum: infinity
Domain:
Certified Tutor
All Algebra II Resources













 is a sine curve. What are the domain and range of this function?
is a sine curve. What are the domain and range of this function?




























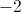

















![[0,100]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218211/gif.latex)




