All Algebra II Resources
Example Questions
Example Question #74 : Solving Logarithms
Solve 
The first thing we can do is move both log functions to one side of the equation:
Then we can combine the log functions (remember, when you add logs, we multiply the terms inside):
Now we can rewrite the equation in exponent form (and FOIL the multiplied terms):
We can collect all the terms on one side of the equation, and then solve the quadratic:
However, if we plug 
Example Question #75 : Solving Logarithms
Solve 
We first put both logs on one side of the equation:
Now we combine the log terms (remember, when we subtract logs we divide the terms inside):
We can now rewrite the equation in exponential form:
Anything raised to the 

Example Question #76 : Solving Logarithms
Solve 
We start by rewriting the equation in exponential form:
Now we can simplify:
Example Question #77 : Solving Logarithms
Solve 
We can either do this the long and proper way, or the simple and easy way.
The long way:
First, we move both logs to the same side of the equation:
Now we can combine the logs (reminder, when you subtract logs, you divide the terms inside of them):
Let's rewrite the equation in exponential form:
Anything raised to the 

The short way:
First, we cancel the log terms (because the base is the same, and all we have are the log terms):
Then we divide by 
Example Question #221 : Logarithms



so in this case it is

and
Example Question #1 : Graphing Logarithmic Functions
Give the 
to two decimal places.
The graph has no 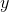
Set 
The 

Example Question #2 : Graphing Logarithmic Functions
Give the 
to two decimal places.
The graph has no 
Set 
The 

Example Question #2 : Graphing Logarithmic Functions
What is/are the asymptote(s) of the graph of the function 


The graph of the logarithmic function
has as its only asymptote the vertical line
Here, since 

Example Question #3 : Graphing Logarithmic Functions
Which is true about the graph of

All of the answers are correct
When 

The range of the function is infinite in both directions positive and negative.
The domain of the function is greater than zero
None of the answers are correct
All of the answers are correct
There is no real number 
Therefore in the equation 

However, 
Finally, when 

Example Question #4 : Graphing Logarithmic Functions
Which of the following is true about the graph of
The range must be greater than zero.
It is an odd function.
The graph is the mirror image of 
The domain is infinite in both directions.
It is an even function.
The graph is the mirror image of 


Certified Tutor
All Algebra II Resources





















































































