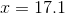Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Other Factorials

Try without a calculator.

10,000 < N! < 100,000

Give the value of that makes this three-part inequality true.

Possible Answers:

N = 9

N = 10

The inequality has no solution.

N = 8

N = 7

Correct answer:

N = 8

Explanation:

Given a nonnegative integer , - or factorial - is defined to be the product of the integers from 1 to . After some exploration, multiplying 1 by 2, the result by 3, that result by 4, and so forth, we find that

$7! = 1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 = 5,040$

Multiplying by 8, we find that

$8! = 1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8= 40,320$

Multiplying by 9, we find that

$9! = 1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9= 362,880$

Therefore,

7! < 10,000 < 8! < 100,000 < 9!

Since only integers may have factorial values, it follows that the only value of that makes the inequality true is N = 8 .

Report an Error

Example Question #95 : Factorials

Try without a calculator:

is equal to which expression?

Possible Answers:

$7! \cdot 7$

7! + 7

7! + 8

$7! \cdot 8$

None of these

Correct answer:

$7! \cdot 8$

Explanation:

- or factorial - is defined to be the product of the integers from 1 to . Therefore,

$7 ! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7$

and

$8 ! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8$

$= (1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7) \cdot 8$

$= 7! \cdot 8$ ,

the correct response.

Report an Error

Example Question #21 : Other Factorials

Try without a calculator:

Which is true about ?

Possible Answers:

is an undefined quantity

Cannot be determined

0! = 0

0! = 1

0!=2

Correct answer:

0! = 1

Explanation:

is considered to be equal to one by definition.

Report an Error

Example Question #97 : Factorials

Try without a calculator:

Calculate:

(3!)!

Possible Answers:

362,880

720

Cannot be determined

120

Correct answer:

720

Explanation:

- or factorial - is defined to be the product of the integers from 1 to . Therefore,

$3! = 1\times 2 \times 3 = 6$

Therefore,

(3!)! = 6!

Since

$6! = 1 \times 2 \times 3 \times 4 \times 5 \times 6 = 720$ ,

it follows that 720 is the correct response.

Report an Error

Example Question #1 : Natural Log

$5^{x}=2e^5$

Solve for .

Possible Answers:

$x = \frac{\textup{ln}2}{\textup{ln}5}$

$x = \frac{\textup{ln}2+5}{\textup{ln}5}$

$x = \frac{\textup{ln}5}{\textup{ln}2+5}$

x=5

Correct answer:

$x = \frac{\textup{ln}2+5}{\textup{ln}5}$

Explanation:

The first thing we notice about this problem is that is an exponent. This should be an immediate reminder: use logs!

The question is, which base should we choose for the log? We should use the natural log (log base e) because the right-hand side of the equation already has e as a base of an exponent. As you will see, things cancel out more nicely this way.

$5^{x}=2e^5$

Take the natural log of both sides:

$\textup{ln}(5^x) = \textup{ln}(2e^5)$

Rewrite the right-hand side of the equation using the product rule for logs:

$\textup{ln}5^x = \textup{ln}2+\textup{ln}e^5$

Now rewrite the whole equation after bringing down those exponents.

$x\textup{ln}5 = \textup{ln}2+5\textup{ln}e$

$\textup{ln}e$ is the same thing as $\textup{log}_{e}e$ , which equals 1.

$x\textup{ln}5 = \textup{ln}2+5$

Now we just divide by $\textup{ln}5$ on both sides to isolate .

$x = \frac{\textup{ln}2+5}{\textup{ln}5}$

Report an Error

Example Question #1 : Natural Log

Rewrite as a single logarithmic expression:

$2 \ln x - \ln (x + 1)$

Possible Answers:

$\ln (x ^{2} - x-1)$

$\ln\frac{ 2x }{x + 1}$

$\ln\frac{ x^{2}}{x + 1}$

$\ln\frac{ x^{2}}{x^{2} +2x+ 1}$

$\ln (x-1)$

Correct answer:

$\ln\frac{ x^{2}}{x + 1}$

Explanation:

Using the properties of logarithms

$n \ln a = \ln a^{n}$ and $\ln a - \ln b = \ln \frac{a}{b}$ ,

we simplify as follows:

$2 \ln x - \ln (x + 1)$

$= \ln x^{2} - \ln (x + 1)$

$= \ln \frac{x^{2} }{x + 1}$

Report an Error

Example Question #1 : Natural Log

Which of the following expressions is equal to the expression $\ln \left ( x^{2} + 4x + 3\right )$ ?

Possible Answers:

None of the other responses is correct.

$\ln x^{2} + \ln 4x + \ln 3$

$\ln x^{2} \cdot \ln 4x \cdot \ln 3$

$\ln (x + 1) + \ln (x + 3)$

$\ln (x + 1) \cdot \ln (x + 3)$

Correct answer:

$\ln (x + 1) + \ln (x + 3)$

Explanation:

By the reverse-FOIL method, we factor the polynomial as follows:

$x^{2} + 4x + 3 = (x + 1)(x + 3)$

Therefore, we can use the property

$\ln ab = \ln a + \ln b$

as follows:

$\ln \left ( x^{2} + 4x + 3\right ) =\ln (x + 1)(x + 3) = \ln (x + 1) + \ln (x+3)$

Report an Error

Example Question #1 : Natural Log

Solve $6e^{-x}+1=3$ . Round to the nearest thousandth.

Possible Answers:

x=-1.099

x=0.089

x=-2.001

x=1.211

Correct answer:

x=-1.099

Explanation:

The original equation is:

$6e^{-x}+1=3$

Subtract from both sides:

$6e^{-x}=2$

Divde both sides by :

$e^{-x}=\frac{2}{6}=\frac{1}{3}$

Take the natural logarithm of both sides:

$-x=\ln \frac{1}{3}$

Divde both sides by and use a calculator to get:

x=-1.099

Report an Error

Example Question #1 : Natural Log

What are the domain and the range of the function f(x)=ln(x) ?

Possible Answers:

Domain = all positive numbers

Range = all positive numbers

Domain = all positive real numbers

Range = all real numbers

Domain = all non-negative numbers

Range = all positive numbers

Domain = all real numbers

Range = all real numbers

Domain = all positive numbers

Range = all non-negative numbers

Correct answer:

Domain = all positive real numbers

Range = all real numbers

Explanation:

Remember that is still a logarithm of a positive number, .

It's not possible to raise to ANY power and obtain a negative number. Because even $e^{-3}$ , for example, is just $\frac{1}{e^3}$ , which is a ratio of two positive numbers, and therefore positive.

More than that, it's also not possible to obtain 0 by raising to any power. Think: "To what power can I exponentiate e and obtain 0?"

So the domain is strictly positive. It excludes negative numbers and 0.

What about the range? To what possible values are we allowed to exponentiate ?

Well, we just saw that e^x has a definition for negative numbers. e^0 = 1 (this fact is true for ALL numbers, not just ).

And we can obviously raise it to positive powers. So the range is all real numbers. It includes negative numbers, 0, and positive numbers.

Report an Error

Example Question #2 : Natural Log

Solve for :

ln(x+3)=3 .

If necessary, round to the nearest tenth.

Possible Answers:

No solution

x=5.7

x=3

x=17.1

x=2.7

Correct answer:

x=17.1

Explanation:

Give both sides the same base, using e:

$e^{ln(x+3)}=e^3$ .

Because e and ln cancel each other out, x+3=e^3 .

Solve for x and round to the nearest tenth:

x=e^3-3

$x\approx17.1$

Report an Error

View Algebra 2 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View Algebra 2 Tutors

Jo
Certified Tutor

Bryn Mawr College, Master's/Graduate, Mathematics. Bryn Mawr College, Bachelor, Mathematics.

View Algebra 2 Tutors

Kathryn
Certified Tutor

Arizona State University, Bachelor of Science, Human Development and Family Studies.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in San Diego, French Tutors in San Francisco-Bay Area, Reading Tutors in Atlanta, GMAT Tutors in Houston, Algebra Tutors in Miami, Physics Tutors in Denver, Physics Tutors in Boston, Physics Tutors in Dallas Fort Worth, Statistics Tutors in San Francisco-Bay Area, Chemistry Tutors in Los Angeles

Popular Courses & Classes

MCAT Courses & Classes in Phoenix, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in Seattle, GRE Courses & Classes in Miami, GMAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in San Diego, MCAT Courses & Classes in Houston, ISEE Courses & Classes in Phoenix, ISEE Courses & Classes in Seattle, ISEE Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in Houston, SSAT Test Prep in Phoenix, LSAT Test Prep in Atlanta, GMAT Test Prep in San Diego, ISEE Test Prep in Phoenix, GMAT Test Prep in Washington DC, GMAT Test Prep in Boston, GMAT Test Prep in New York City, SSAT Test Prep in Chicago, GRE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #21 : Other Factorials

Example Question #95 : Factorials

Example Question #21 : Other Factorials

Example Question #97 : Factorials

Example Question #1 : Natural Log

Example Question #1 : Natural Log

Example Question #1 : Natural Log

Example Question #1 : Natural Log

Example Question #1 : Natural Log

Example Question #2 : Natural Log

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: