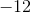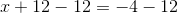Multiply the bottom equation by , then add to the top equation:

Divide both sides by 

When we add the two equations, the  variables cancel leaving us with:

Solving for  we get:

We can then substitute our value for  into one of the original equations and solve for :

We are given

We can solve this by using the substitution method.  Notice that you can plug  from the first equation into the second equation and then get

Add  to both sides

Add 9 to both sides

Divide both sides by 5

So . We can use this value to find y by using either equation. In this case, I'll use .

So the solution is 

Let  be the number of adult tickets sold. Then the number of child tickets sold is .

The amount of money raised from adult tickets is ; the amount of money raised from child tickets is . The sum of these money amounts is , so the amount of money raised can be defined by the following equation:

To find the number of adult tickets sold, solve for :

 adult tickets were sold.

Let's call "" the cost of one jersey (this is the value we want to find)

Let's call the amount of money Jack starts with ""

Let's call the amount of money Aaron starts with ""

We know Jack buys a glove for  and  bats for  each, and then has  left over after. Thus:

simplifying,  so Jack started with 

We know Aaron buys  hats for  each and  jerseys (unknown cost "") and spends all his money.

The last important piece of information from the problem is Aaron starts with  dollars more than Jack. So:

From before we know:

Plugging in:

so Aaron started with 

Finally we plug  into our original equation for A and solve for x:

Thus one jersey costs 

Use the elimination process to determine the value of .

Subtract the second equation with the first equation.  This will eliminate the x-variable in order to find the y-variable.

The equation becomes:  

Use this value and substitute into either the first or second equation and solve for the x-variable.

Let's select the first equation and solve for .

Add six on both sides.

The result will be the same if we substitute  into the second equation.

The answer is:  

In order to solve for , multiply the first equation by four in order to eliminate the fractions in front of the coefficients.

The first equation becomes:

The second equation remains the same:  

Subtract the second equation with the first equation:

The result is:  

Divide by two on both sides.

Simplify both sides.

The answer is:  

In order to solve for the  variable, we will need to use the elimination method.

Subtract the first equation with the second equation in order to eliminate the  variable to solve for .

After subtracting equation one with equation two:

Use this value and either equation to solve for . Let's choose the first equation.

Subtract twelve from both sides.

Simplify both sides.

The answer is: 

6,035 total tickets were sold, and the total number of tickets is the sum of the adult and child tickets, .

Therefore, we can say .

The amount of money raised from adult tickets is $11 per ticket mutiplied by  tickets, or  dollars; similarly,  dollars are raised from child tickets. Add these together to get the total amount of money raised:

These two equations form our system of equations.

This system can be solved a variety of ways, including graphing. To solve algebraically, write an equation for each of the different trains. We will use y to represent the distance from San Francisco, and x to represent the time since 8AM.

The blue train travels 80 miles per hour, so it adds 80 to the distance from San Francisco every hour. Algebraically, this can be written as .

The green train starts 380 miles away from San Francisco and subtracts distance every hour. This equation should be .

To figure out where these trains' paths will intersect, we can set both right sides equal to each other, since the left side of each is .

add  to both sides

divide both sides by 140

Since we wrote the equation meaning time for , this means that the trains will cross paths after 2.714 hours have gone by. To figure out what time it will be then, figure out how many minutes are in 0.714 hours by multiplying . So the trains intersect after 2 hours and about 43 minutes, so at 10:43AM.

To figure out how far from San Francisco they are, figure out how many miles the blue train could have gone in 2.714 hours. In other words, plug 2.714 back into the equation , giving you an answer of .