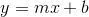Begin by calculating the slope of Line 1 as 

.

Now, realize that since Line 2 is perpindicular to Line 1, the slope of Line 2 is the negative reciprocal of the slope of Line 1.

Therefore, the slope of Line 2 is given as 

.

We also know that Line 2 passes through point (8,5).

Therefore, we may use "point-slope" form to express the equation of Line 2 as: 

.

Finally, convert this "point-slope" equation to "slope-intercept" form in order to match the result with the correct answer choice: 

. 

When finding the slope of a perpendicular line, we need to ensure we have  form.    stands for slope. Our  is . To find the perpendicular slope, we need to take the negative reciprocal of that value which is . Since we are looking for an equation, we need to reuse the  form to solve for  . We do this by plugging in our coordinates. 

 Add  on both sides.

Our equation is now .

When finding the slope of a perpendicular line, we need to ensure we have  form.  Let's rearrange it. By subtracting  on both sides and dividing  on both sides, we get .  stands for slope. Our  is . To find the perpendicular slope, we need to take the negative reciprocal of that value which is . Since we are looking for an equation, we need to reuse the  form to solve for  . We do this by plugging in our coordinates. 

 Subtract  on both sides.

Our equation is now .

When finding the slope of a perpendicular line, we need to ensure we have  form.  Let's rearrange it. By add  on both sides and dividing  on both sides, we get .  stands for slope. Our  is . To find the perpendicular slope, we need to take the negative reciprocal of that value which is . Since we are looking for an equation, we need to reuse the  form to solve for  . We do this by plugging in our coordinates. 

 Add  on both sides.

Our equation is now .

Perpendicular lines have slopes that are opposite reciprocals meaning that the slope is flpped. The equation that satisfies both of these criteria is:

Write the points that correspond to the x and y-intercepts given in the problem.

X-intercept of one: 

Y-intercept of two: 

Find the slope of this line connected with these points.

The slope is negative two. The slope of the perpendicular line is the negative reciprocal of this slope.

Write the slope-intercept form.

Substitute the perpendicular slope with the point that this line will pass through.

Solve for the y-intercept, .

Subtract nine halves on both sides.

Simplify both sides.

With the perpendicular slope and the y-intercept, write the equation of the line.

The answer is:

Step 1: get the line into y = mx +b format to find the slope m:

Next, we need to remember that perpendicular lines have slopes that are negative reciprocals. Find the negative reciprocal of :

First, you should plug the given points, (5, –8) (–2, 6), into the slope formula to find the slope of the line. 

Then, plug the slope into the slope formula, y = mx + b, where m is the slope.

y = –2x + b

Plug in either one of the given points, (5, –8) or (–2, 6), into the equation to find the y-intercept (b). 

6 = –2(–2) + b

6 = 4 + b

2 = b

Plug in both the slope and the y-intercept into slope intercept form. 

y = –2x + 2

These lines are written in the form y = mx + b, where m is the slope and b is the y-intercept. We know from the question that our slope is 3 and our y-intercept is –5, so plugging these values in we get the equation of our line to be y = 3x – 5.

m = 3 and b = –5

is the slope-intercept form of the equation of a line.

Slope  is equal to  between points, or .

So .

At point (8, 3 ) the equation becomes

So