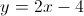Use the point-slope formula to find the equation:

Start by using point-slope form:

Multiply the right side by the distributive property:

Then, convert to standard form:

Slope-intercept form is , where  is the slope and  is the y-intercept.  To rewrite the original equation in slope-intercept form, you must isolate the  variable: 

Now, divide each side by 20 so that  stands alone and simplify, and you are left with the slope-intercept form of the equation:

Let .

First, calculate the slope between the two points.

Next, use the slope-intercept form to calculate the intercept. We are able to plug in our value for the slope, as well the the values for .

Using slope-intercept form, where we know and , we can see that the equation for this line is .

To find the equation of this line, we need to know its slope and y-intercept. Let's find the slope first using our general slope formula.

The points are  and .  In this case, our points are (–3,0) and (2,5). Therefore, we can calculate the slope as the following:

Our slope is 1, so plug that into the equation of the line:

We still need to find b, the y-intercept. To find this, we pick one of our points (either (–3,0) or (2,5)) and plug it into our equation. We'll use (–3,0).

Solve for b.

The equation is therefore written as .

The equation for a line takes the form where m is the slope and b is the y-intercept, where the graph hits the y-axis.

The y-intercept of this line is 1, so b=1.

We can figure out the slope by comparing how far the line goes up vs. how far it goes over between any 2 points. The two most obvious points on the graph are at and . Between these two points, the graph moves down 1 and over 5. This means the slope is , so we'll put that in for m.

The equation is then .

The equation for a line takes the form where m is the slope and b is the y-intercept, where the graph hits the y-axis.

The y-intercept of this line is -4, so b=-4.

We can figure out the slope by comparing how far the line goes up vs. how far it goes over between any 2 points. The two most obvious points on the graph are at  and . Between these two points, the graph moves up 3 and over 5. This means the slope is , so we'll put that in for m.

The equation is then .

We are given the slope and a point, which we will plug into .

.

Thus, using the given  and the  you just found, the equation of our line is:

The equation for a line is always , where  and .

Given two data points, we are able to find the slope, m, using the formula 

.

Using the data points provided, our formula will be: 

, which gives us  or , .

Our y-intercept is given.

Thus our equation for the line containing these points and that y-intercept is .

The equation of a line is , where "m" is the slope of the line and "b" is the point at which the line intercepts the y-axis. 

The first thing we must do is use the formula 

to find the slope, or "m."

If we plug in the points of the two coordinates given, 

,

we find our slope, "m."

Since our y-intercept is given, we now have everything we need for our equation, 

.