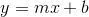Write the points that correspond to the x and y-intercepts given in the problem.

X-intercept of one: 

Y-intercept of two: 

Find the slope of this line connected with these points.

The slope is negative two. The slope of the perpendicular line is the negative reciprocal of this slope.

Write the slope-intercept form.

Substitute the perpendicular slope with the point that this line will pass through.

Solve for the y-intercept, .

Subtract nine halves on both sides.

Simplify both sides.

With the perpendicular slope and the y-intercept, write the equation of the line.

The answer is:

Step 1: get the line into y = mx +b format to find the slope m:

Next, we need to remember that perpendicular lines have slopes that are negative reciprocals. Find the negative reciprocal of :

First, you should plug the given points, (5, –8) (–2, 6), into the slope formula to find the slope of the line. 

Then, plug the slope into the slope formula, y = mx + b, where m is the slope.

y = –2x + b

Plug in either one of the given points, (5, –8) or (–2, 6), into the equation to find the y-intercept (b). 

6 = –2(–2) + b

6 = 4 + b

2 = b

Plug in both the slope and the y-intercept into slope intercept form. 

y = –2x + 2

These lines are written in the form y = mx + b, where m is the slope and b is the y-intercept. We know from the question that our slope is 3 and our y-intercept is –5, so plugging these values in we get the equation of our line to be y = 3x – 5.

m = 3 and b = –5

is the slope-intercept form of the equation of a line.

Slope  is equal to  between points, or .

So .

At point (8, 3 ) the equation becomes

So

The slope of the line passing through points  and  can be computed as follows:

Now, the new line, since it is parallel, will have the same slope.  To find the equation of this new line, we use point-slope form:

, where  is the slope and  is the point the line passes through.

After rearranging, this becomes

When finding the equation of a line from some of its points, it's easiest to first find the line's slope, or .

To find slope, divide the difference in  values by the difference in  values. This gives us  divided by , or .

Next, we just need to find , which is the line's -intercept. By plugging one of the points into the equation , we obtain a  value of 11 and a final equation of

We can find the equation of th line in slope-intercept form by finding and .

First, calculate the slope, , for any two points. We will use the first two.

Next, using the slope and any point on the line, calculate the y-intercept, . We will use the first point.

The correct equation in slope-intercept form is .

When a line is in the  format, the  is its slope and the  is its -intercept. In this case, the equation with a slope of  and a -intercept of  is .

We can treat the price of the stock as the value and the year as the value, making any points take the form , or . This question is asking for the line that includes points  and . 

To find the equation, first, we need the slope.

Now use the point-slope formula with this slope and either point (we will choose the second).