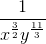All Algebra 1 Resources
Example Questions
Example Question #573 : Variables
Simplify: 
What is the exponent of 
1, in the numerator
2, in the denominator
2, in the numerator

1, in the denominator
1, in the denominator
The exponent of 
Example Question #157 : Monomials
Simplify: 
What is the exponent of 

2, in the numerator
1, in the denominator
2, in the denominator
1, in the numerator
2, in the numerator
To simplify this expression use the law of exponents which state that when a term is raised to a power, multiply the exponents. Also, when terms of like bases are divided the exponents are subtracted.
The exponent of 
Example Question #152 : Monomials
Simplify the expression

What is the coefficient in this expression after it is simplified?
To simplify the expression use the rule of exponents which states that when like bases are raised to a power the exponents are multiplied together. When like bases are divided that means that their exponents are subtracted.
The coefficient of this simplified form is 
Example Question #159 : Monomials
Simplify:
In order to simplify, rewrite the numerator in terms of exponential powers.
Because similar bases are divided, subtract the powers of the numerator with the denominator.
Since these two variables have negative exponents, we can simply take the inverse of both to eliminate the negative exponents.
Multiply both fractions.
The answer is:
Example Question #32 : Quadratic Equations
What is the equation that has the following solutions?
This is a FOIL-ing problem. First, set up the numbers in a form we can use to create the function.
Take the opposite sign of each of the numbers and place them in this format.
Multiply the 

Multiply the 


Then add them together to get
Combine like terms to find the answer which is 
Example Question #4811 : Algebra 1
Simplify the following expression.
Simplify using FOIL method.
Remember that multiplying variables means adding their exponents.
F:
O:
I:
L:
Combine the terms. Note that we cannot simplify further, as the exponents do not match and cannot be combined.
Example Question #1 : Distributive Property

Example Question #1 : Distributive Property
What are the factors of 
To find the factors, you must determine which of the sets of factors result in the polynomial when multiplied together. Using the FOIL method, a set of factors with the form 





Example Question #5 : How To Use Foil In The Distributive Property
Expand:
If you use the FOIL method, you will multiply each expression individually. So, 


Example Question #3 : Distributive Property
Simplify the expression below.
Use the distributive property to simplify the expression. In general, 
Now we can begin to combine like terms through multiplication.
We cannot simplify further.
Certified Tutor
Certified Tutor
All Algebra 1 Resources

























![\frac{\sqrt{x} \cdot \sqrt[3]{y}}{x^2y^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/714747/gif.latex)



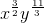

![\frac{\sqrt{x} \cdot \sqrt[3]{y}}{x^2y^4} = \frac{x^{\frac{1}{2}} y^{\frac{1}{3}}}{x^2y^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/714748/gif.latex)