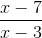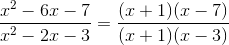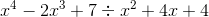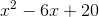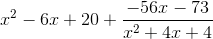Once simplified, (x+1) appears on both the numerator and denominator, meaning we can cancel out both of them.

Which gives us:

 can be divided using long division. 

The set up would look very similar to the division of real numbers, such as when we want to divide 10 by 2 and the answer is 5.

The first step after setting up the "division house" is to see what the first term in the outer trinomial needs to multiplied by to match the 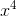 in the house. In this case, it's .  will be multiplied across the other two terms in the outer trinomial and the product will be subtracted from the expression inside the division house. The following steps will take place in the same way. 

While we could continue to divide, it would require the use of fraction exponents that would make the answer more complicated. Therefore, the term in red will be the remainder. Because this remainder is still subject to be being divided by the trinomial outside of the division house, we will make the remainder part of the final answer by writing it in fraction form:

Therefore the final answer is

The polynomial factors to (3y-4)(y+6).  (y+6) is the only one of those two options available as an answer.

First, write as a sum of the cubes,     

 x³ + 3³,  then factor : (x + 3) (x² – 3x + 3²).  Apply the exponent:

(x + 3) (x² – 3x + 9)

2x² + ab – 2b – ax² = 2x² – 2b – ax² + ab           

Rearrange  terms

= (2x² – 2b) + (- ax² + ab)   Group

= 2(x² – b) + a(-x² + b)        Factor each group

= 2(x² – b) – a(x² – b)          Factor out  -a

= (x² – b) (2 – a)                  Factor out x² – b

Factor the polynomial by choosing two values that when FOILed will sum to the middle coefficient, 3, and multiply to 2.  These two numbers are 1 and 2.

Only (x +1) is one of the choices listed.

The polynomial factors into the following expression:

Therefore, the answer is 

You have two options for a problem like this. On the one hand, you can merely FOIL the answers until you find one that equals the value given in the equation. The other option is to factor it adequately from the beginning. This is not too hard. Since the middle term is so small, you know that the numeric portions of your factors will have to be nearly equal. Since we know that , this is very easy! Given that the last value is a negative number, you know that your two groups need to be a combination of addition and subtraction. 

Thus, your answer is: 

You have two options for a problem like this. On the one hand, you can merely FOIL the answers until you find one that equals the value given in the equation. The other option is to factor it adequately from the beginning. For a question like this, it is a bit harder, given that there is a number in front of the first term. Now, given the signs in the original problem, you know that your groups will look like the following:

Now, you can do a little trick to make your life easier. Factor out the common :

The latter is very easy to factor:

Now, you have:

You can distribute the  into either group. For the answers given, the only correct value is:

You have two options for a problem like this. On the one hand, you can merely FOIL the answers until you find one that equals the value given in the equation. The other option is to factor it adequately from the beginning. This is not too hard. You know that your groups will need to have one positive and one negative between them (this is because of the  at the end of your original polynomial). Now, you need to carefully pick your factors. It certainly is not  and ; however, neither will  and  nor  and  work. Notice that  and  does the trick: